摘要： 应用Soildworks 建立高效立式加工中心立柱数字化模型,运用Simulation 对立柱进行有限元分析，获得立柱的静、动态特性参数。综合运用正交试验设计、模糊数学和有限元分析理论，对立柱的结构参数进行多目标模糊优化，获得最优结构参数为壁厚22 mm、肋板厚18 mm、顶部开窗大小140 mm×320 mm。分析表明，优化后立柱位移减小6%，1 阶固有频率增加1.2%。通过对立柱结构参数的优化，提高了其静、动态特性。

  
         
     1 、立柱结构模型的建立

     采用三维建模软件Solidworks 建立加工中心立柱数字化模型，并且为了能方便地在进行结构分析时获得有效地计算结果，同时又能保证分析速度以及分析精度，首先对立柱模型进行结构简化，去掉立柱结构中对分析影响不大的凸台、螺纹孔以及倒角，进而得到简化的立柱数字化模型，如图1 所示*河北省科技支撑计划资助项目（11212110D） 。

     图1 立柱数字化模型

     2 、立柱静、动态性能分析

    （1）单元选取及网格划分

     立柱的参数设定：材料为HT250，各向同性，介质均匀，弹性模量E=130 GPa，泊松比γ=0.25，密度ρ=7.4 g/mm3，由于加工中心立柱的结构复杂，所以网格划分将采用Solidworks Simulation 中网格智能划分方法，同时为了能够减少单元数量，提高分析速度，选用高品质单元，划分后节点总数为93 626，单元数为52 494。

     （2）立柱的静态分析

      静态分析是计算在固定载荷作用下结构产生的位移、应力以及应变，而且不需要考虑惯性和阻尼的影响。在进行有限元分析时约束施加在立柱底部与床身接触的4 个方形区域，立柱所受工作载荷主要是主轴箱的重力和切削力。以钻孔为典型工况，立柱受力如图2 所示，沿X 轴方向的载荷分别为：Fx1=Fx2=177.9 N、Fx3=Fx4=233.1 N， 沿Y 轴方向的
载荷分别为：Fy1=Fy2=277.1 N、Fy3=Fy4=-266.1 N，以及沿Z 轴方向的载荷Fz=271.4 N。

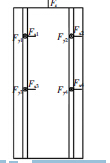
      图2 立柱受力图
 

      将数字化模型导入Solidworks Simulation，便可进行求解运算，求解后的立柱位移云图如图3、图4所示。由图3、图4 可以看出X 向位移变化量最大，其最大变形量为6.55e-4 mm，并且发生在立柱的垂直壁上，而Y 向变形较小，可以忽略，因此可以通过改变肋板厚、立柱壁厚以及改变肋板布局来提高立柱的刚度。

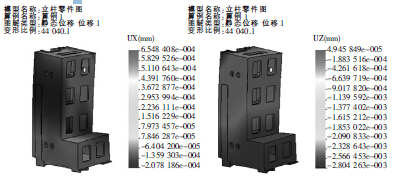
                 图3 X 向变形量                       图4 Y 向变形量

     （3）立柱的动态分析

      动态性能分析可以反映出结构的2 个振动特性参数，即固有频率和振型，这2 个特性是动态分析中2 个重要的参数，因在动态性能分析中与载荷无关，因而能够充分体现结构特性，并且可以从分析结果中看出其结构的薄弱环节，从而为结构优化提供依据。

      模态分析中该立柱的约束施加在立柱底部与床身接触的4 个方形区域。立柱的振动是由各阶振型的线性叠加， 其低阶振型比高阶振型影响大，越是低阶影响越大，低阶振型对立柱的动态性能起决定作用，因此，取立柱的前5 阶模态振型进行动态性能分析。

      将数字化模型和约束导入Solidworks Simulation，便可进行求解运算，运行计算后，可得到立柱的前5阶固有频率和振型，如图5～图9 所示。

                  图5   1 阶振型                         图6 2 阶振型

                   图7   3 阶振型                    图8 4 阶振型
 

                              图9   5 阶振型

   
      由图5～图9 可知，前5 阶固有频率分别为146.48Hz、164.43 Hz、300.59 Hz、434.27 Hz、446.24 Hz；第1阶振型主要表现为立柱上部沿X 轴摇摆振动； 第2阶振型主要表现为立柱上部沿Y 轴摇摆振动； 第3阶振型主要表现为立柱沿Z 轴扭转振动；第4 阶振型主要表现为在中间开窗部分做内凹振动；第5 阶振型类似于第3 阶振型。可见第1、第2、第4 阶振型为局部振动，而第3、第5 振型为整体振动。第1、第2 阶振型的固有频率较低，可通过强化立柱刚度来提高的动态性能。

      3 、立柱结构参数优化

      通过对加工中心立柱的静、动态性能分析可知，其影响因素主要有立柱的刚度、主轴箱的重量、工况、切削载荷和立柱材料等。若改善立柱的静、动态性能，最有效的方法就是提高立柱的刚度。

      （1）立柱设计方案的确定

      立柱的刚度与截面形状和尺寸有关，而影响立柱的截面形状和尺寸因素很多，选择截面形状和尺寸较优的立柱，就成为一件非常繁琐的工作。采用正交试验法，将会降低试验次数，从而减少一些不必要的工作量。①选择立柱壁厚、肋板厚、顶部开窗大小作为正交试验的3 个因素；②根据每一设计参数的范围内选取3 个不同水平的值；③选取正交试验表L9（34），由此确定9 个正交设计方案如表1 所示。

                                   表1 正交试验方案

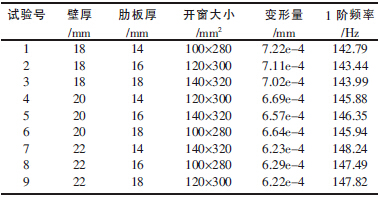
      应用Solidworks 分别建立9 个方案的立柱数字化模型，然后导入有限元分析软件Solidworks Simulation进行求解运算，得出9 个方案立柱的动静态特性分析结果即变形量与1 阶频率如表1 所示。

      （2）立柱参数多目标模糊优化

      多目标模糊优化理论是在基于求解各单目标问题满意解的基础上寻求多目标最优解，能够充分体现它们之间的相互关系，可以较好地兼顾多个目标，且各目标之间的相对重要性可以通过权重加以体现。

     为了综合考虑各因素对立柱结构的影响，现以模糊综合评价值作为综合评价指标。以变形量、1 阶频率为评价指标集U=｛Y1，Y2｝。以正交试验设计的9 个设计方案为评价对象集，D＝｛d1，d2，…，d9｝。建立评价指标集U 对评价级V 的隶属函数，使根据隶属函数计算得到的隶属度值的大小与该指标在综合评价中的重要性相适应， 隶属函数为单调函数，隶属度rmn在0~1（m=1，2，3），（n=1，2，…，9）。其中，变形量Y1n为偏小型指标， 隶属函数为r1n   =  

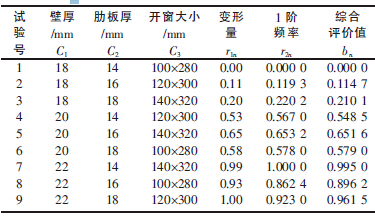
                          表2 单指标的隶属度值和模糊综合评价值

      A 是指标集U 上的模糊子集， 称为权重分配集，它反映各指标的重要程度。在立柱设计中，变形量和1 阶频率直接影响其加工的精度，各取权重为0.5。由此模糊子集A 确定为：A=｛0.5/Y1，0.5/Y2｝，简记为：A＝｛0.5，0.5｝。

      在评价集V 上引入一个模糊子集B，称为评价级，它的模糊评价B=｛b1，b2，…，b9｝，由模糊矩阵R与权重分配集A 经模糊变换得到：B=AoR。模糊运算方法有多种，采用M（·，+）算子对B=AoR 进行模糊变换， 得到综合评价模糊子集B 的隶属度bn，即模糊综合评价值，如表2 所示。
 
      由主效应分析计算，可知3 个设计参数对立柱综合性能的影响程度从大到小依次为壁厚、顶部开窗大小、肋板厚；由两因素之间的交互效应分折可知，壁厚与开窗大小的交互效应最大；由全部因素各水平搭配的交互效应分析可知， 在全部可能的3种因素各水平搭配中，壁厚22 mm、肋板厚18 mm、开窗大小140 mm×320 mm 对综合评价值的影响最大。
因此在考虑交互作用情况下，这种参数组合得到的综合评价值最好。
 
 
     （3）优化后立柱结构性能分析

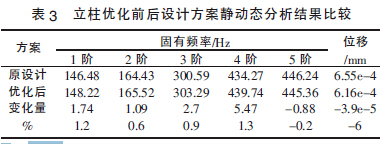
     根据模糊综合评价值最好的立柱设计参数：壁厚22 mm、肋板厚18 mm、开窗大小140 mm×320 mm，应用Solidworks 建立该方案的立柱数字化模型，并导入有限元分析软件Solidworks Simulation 中进行有限元静、动态特性分析。根据优化前、后立柱结构的有限元分析结果，将最大变形量、1 阶固有频率几个最重要的指标汇总如表3 所示。

       由表3 结果表明，优化后的立柱结构与优化前设计结构最大位移减小了6%，1 阶固有频率增加了。
 

      4、 结语

      应用Simulation 有限元分析软件， 对所设计的高效立式加工中心立柱进行了静、动态特性分析，获得了立柱在不同方向上的受力变形，通过对立柱的固有频率及振型的分析，获得了立柱的动态特性参数。综合运用正交试验设计、模糊数学和有限元分析理论，对立柱的结构参数进行了多目标模糊优化。分析表明，通过Soildworks Simulation 有限元分析方法对加工中心立柱进行静、动态特性分析，可以快速有效地确定立柱结构参数的最优方案，缩短产品的试验周期以及大量的试验和计算工作， 为机床结构优化设计提供了一种新的途径。