基于指数函数的机床主轴热误差补偿模型
2017-12-15 来源: 山东大学机械工程学院 山东永华机械 作者:王乾俸 张松 陈舟 张宝雷 江诚
摘 要:在对机床主轴进行热特性分析的基础上,建立了基于指数函数的机床主轴轴向热误差补偿模型。该热误差补偿模型建模时间短、资金成本低,能够方便快捷地应用到工厂生产环境中。通过实验获得不同转速下的主轴轴向热变形数据。使用回归分析和最小二乘法建立了稳定状态下主轴轴向变形量和时间常数的估计方程,进而建立了基于指数函数的热误差补偿模型。该模型可以预测不同转速下主轴的轴向变形量。通过实验证明了该热补偿模型在机床主轴恒速运转和变速运转两种工况下均具有较高的精度。
关键词:热补偿模型;热变形;指数函数;机床热特性
0、引言
机床热误差是指由机床热变形导致的加工误差或运动误差。热误差是影响数控机床加工精度的主要误差源之一[1]。机床内部产生的热量和环境温度梯度致使机床温度场复杂多变。随着机床几何定位精度和加工性能的提高,热变形误差严重影响了机床精度。
通常抵消热误差的方法主要包括热稳定性设计、温度控制和热误差补偿三种方法[2]。热稳定性设计是指通过采用新型材料改进设计方法和制造工艺,提高机床精度和刚度,以降低加工误差。然而,当机床精度达到一定程度后,提高机床精度的难度较大且成本较高。温度控制一般是指使用相关技术来控制机床温度。但是温度控制总是滞后于温度升高,即只有温度变化后才能进行控制。热误差补偿则是对由于温度波动引起的零件尺寸变化进行补偿。该方法不被限制于机床的设计阶段,可以提高已有机床的加工精度,因此越来越受到重视。由于机床主轴在高速运转下将产生大量的热量,机床的加工精度在很大程度上依赖于机床主轴的精度[3]。对主轴热变形影响最大的因素是主轴前后轴承的摩擦热。当主轴旋转时主轴前后轴承摩擦生热,产生的热量传递到主轴和刀柄等,导致主轴系统的热变形,从而影响机床的加工精度。因此,对主轴系统的热误差进行补偿至关重要。
在热误差补偿中热误差模型的建立是关键环节。最常见的热误差建模方法主要有两种:①统计回归建模法,即根据统计理论对热误差数据和机床温度值进行相关分析,用最小二乘原理进行拟合建模[4-5],统计回归法是以系数的形式表现机床的特征信息;②神经网络建模法[6],从理论上说,神经网络能以任意精度逼近任意非线性映射,但神经网络建模法需要大量的数据用于训练神经网络,该建模方法需要花费大量的时间用于数据采集和模型训练[7-8]。由于建模成本高且传感器安装困难,这两种建立热误差补偿模型的方法通常不会被采纳[9]。
本文提出一种基于主轴转速的热误差模型。该模型只需主轴转速、无需温度数据,就可以预报机床的热误差。主轴转速能够通过工件的NC加工程序得到,因此补偿工作可以与编制加工程序一并进行,从而无需添加任何硬件设备就可实现机床的热误差补偿。该模型具有预报精度高、能够方便快捷地应用于工厂环境的特点。本文首先通过机床热特性分析实验测量主轴的轴向热变形数据,然后根据实验分析结果建立基于指数函数的热误差补偿模型,最后使用该模型对机床主轴恒速运转和变速运转两种工况下的机床主轴轴向变形量进行补偿。结果表明,该模型在这两种不同工况下均具有较高的精度。
1、 机床主轴热误差测试及分析
为了进行机床主轴热特性分析,首先通过实验测量机床在不同转速下空转时主轴的轴向热变形量、主轴轴端温度和机床环境温度。实验装置如图1所示,使用东华DH904 电涡流位移传感器和Pt100铂电阻温度传感器,测量韩国大宇立式加工中心主轴的热变形数据。电涡流位移传感器用于测量主轴的轴向热变形量,铂电阻温度传感器用于测量主轴的轴端温度和机床环境温度。表1和表2分别为立式加工中心和电涡流位移传感器的规格参数。

图1 试验装置
表1 立式加工中心规格参数

表2 DH904电涡流位移传感器规格参数

测量不同转速下主轴的轴向变形量,步骤如下:
(1)主轴在2 000r/min转速下空转,直到主轴轴向变形量达到稳定状态。
(2)主轴停止运转,直到主轴轴端温度回到初始值。
(3)使用信号采集系统记录以上过程中的主轴轴向变形量和主轴轴端温度以及环境温度。
(4)在主轴转速分别为2 500,3 000,3 500,4 000,4 500,5 000,5 500,6 000r/min下,重复以上步骤。
图2为不同转速下主轴的轴向变形量随时间的变化曲线。从图中可以看出:在机床主轴运转的初始阶段,主轴轴向变形量的增长速度均较快,随着机床主轴的运转,主轴轴向变形量的增长速度逐渐变缓,并且在7 200s左右时主轴轴向变形量均基本达到稳定状态。图3所示为主轴轴端温度随时间的变化曲线。从图中可以看出:不同转速n 下主轴轴端的温度在7 200s左右时也基本达到稳定状态。图4所示为主轴轴端温升变化曲线。从图中可以看出:主轴转速n越大,主轴轴端温升越大。图5所示为不同转速下机床主轴热变形达到稳定状态后机床主轴的轴向热变形量。从图5可以看出,稳定状态后机床主轴的轴向变形量与主轴转速呈近似线性关系。基于以上分析,可以发现主轴的轴向变形量Δz随运转时间t的变化情况基本符合先快后慢再稳定的自然指数模型增长规律。
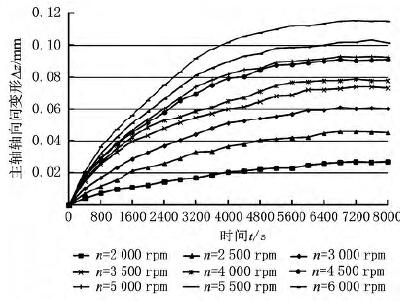
图2 不同转速下主轴的轴向变形量
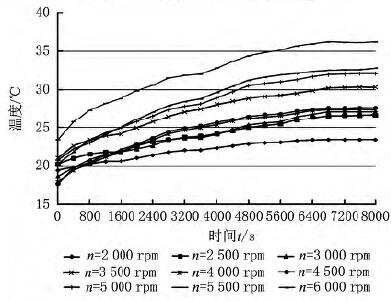
图3 不同转速下主轴的轴端温度
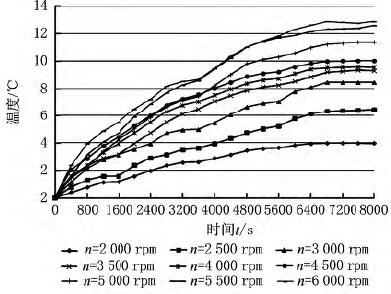
图4 不同转速下主轴的轴端温升
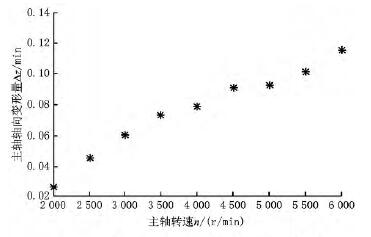
图5 文档状态下不同转速对应的主轴的轴向变形量
2 、主轴热误差补偿模型及验证
2.1 主轴热误差补偿模型
根据机床主轴热特性实验的分析结果,可以建立一种基于指数函数的热误差补偿模型,以补偿主轴轴向热变形量。热误差补偿模型的基本形式如下[10]:

为确定zs的表达式,使用实验数据建立了zs的估计方程。使用回归分析和最小二乘法进行直线拟合,以表达稳定状态下的主轴轴向变形量和主轴转速n、稳定状态主轴轴端温度与初始温度之差ΔT的线性关系。拟合直线公式如式(2)所示。



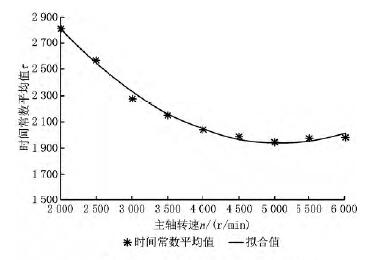
图6 时间常数均值--主轴转速拟合曲线
2.2 实验验证
为验证该热误差补偿模型的精度,对主轴恒速运转和主轴变速运转两种工况下的主轴轴向变形量进行补偿。每种工况下分别测量主轴空转时的主轴轴向变形量和铣削铝合金工件的加工尺寸。
2.2.1 主轴恒速空运转
在主轴恒速空转工况下测量主轴的轴向变形量,即:使机床分别在2 400r/min、4 400r/min转速下运转8 000s,记录该过程中的主轴轴向变形量。图7为主轴轴向变形量随时间的变化曲线,以及对主轴轴向变形量的预测曲线。由图7可知,2400r/min转速下补偿前主轴的轴向最大误差为0.043 72mm,补偿后的最大误差为0.004mm,精度提高了92%;4 400r/min转速下补偿前主轴的轴向最大误差为0.087 34mm,补偿后的最大误差为0.007 92mm,精度提高了90.7%。由此证明,在主轴恒速空转时该模型具有较高的精度。
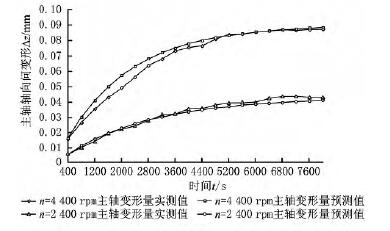
图7 主轴恒速空转模型预测结果
2.2.2 主轴恒速切削
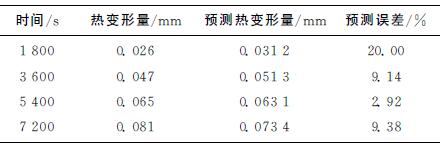
使机床恒速运转切削铝合金,通过测量工件的加工误差判定机床主轴热变形量的大小。本实验使用300mm×46mm×17.3mm的铝合金方块作为实验样本,表3为铝合金材料参数。本实验中使用带有循环可转位刀片的立铣刀,铣刀直径为20mm。图8为切削实验装置,表4为切削参数。工件加工误差除了包括热误差,还包括机床几何误差、定位误差以及测量误差等,因此以初始时刻(t=0)加工槽底面作为基准,分别测量后续加工槽底面与基准之间的距离,作为因主轴热变形而导致的加工误差。表5和表6分别为2 400、4 400r/min转速下的机床主轴热变形量、模型预测热变形量和预测误差,根据表5和表6可以证明该模型在主轴恒速切削情况下的补偿精度较高。例如:主轴转速为2 400r/min时补偿前的最大热变形量为0.053mm,补偿后的热变形量为0.012 8 mm,机床精度提高75.8%。主轴转速为4 400r/min时补偿前的热变形量为0.079mm,补偿后的热变形量为0.013 7mm,机床精度提高82.7%。由于机床切削过程中功率增大、轴承负载增大导致主轴系统产热增加,并且测量工件尺寸时不能排除测量误差、定位误差和机床振动等对测量数据的影响,切削条件下模型精度必然降低。

图8 铣削试验装置
表3 铝合金材料参数

表4 铣削参数
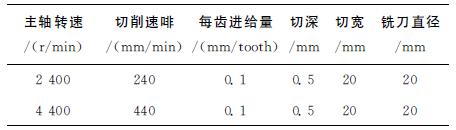
表5 2 400r/min转速下工件误差及其预测值
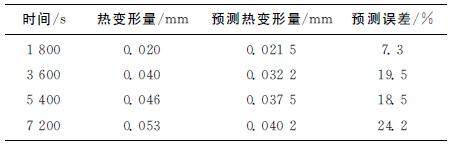
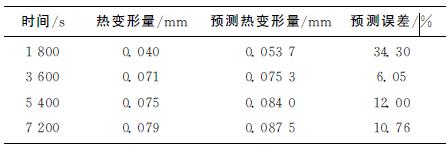
表6 4 400r/min转速下工件误差及其预测值
3.2.3 主轴变速空运转
在主轴变速空转工况下测量主轴的轴向变形量,即:使机床按照图9所示的转速运转,记录该过程中的主轴轴向变形量。图10为主轴轴向变形量的实际值和预测值,误差补偿前最大误差为0.088 6mm,补偿后最大误差为0.005 2mm,主轴精度提高了约94%。由此证明,该热误差补偿模型在变速空转情况下仍具有较高的精度
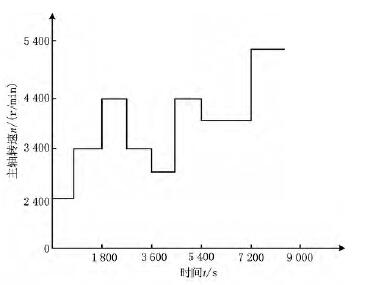
图9 主轴变色试验
3.2.4 主轴变速切削
在与主轴恒速切削实验相同的条件下进行主轴变速切削实验。主轴转速变化情况与图9一致,铣削参数和刀具均与主轴恒速切削工况一致。表7为机床主轴热变形量、模型预测热变形量和预测误差。表7表明,该模型在主轴变速切削情况下也具有较高的精度,补偿前机床最大热变形量为0.082mm,补偿后最大热变形量为0.008 6mm,机床精度提高了89.5%。但是与主轴空转下进行补偿的结果相比,切削情况下的补偿精度也有所降低。
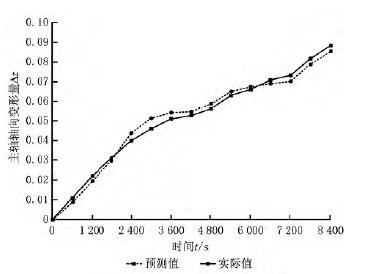
图10 主轴变色空转工况模型预测结果
表7 变速切削工况下工件误差
3、 结束语
本文在对机床主轴系统进行热特性分析的基础上,建立了基于指数函数的热补偿模型,并进行了实验验证。本文的主要工作及相应结论如下:
(1)通过测试数控加工中心主轴的轴向热变形量和轴端温度,对机床主轴进行热特性分析后可知,在不同转速下,机床主轴在运行7 200s后均基本达到稳定状态,稳定状态后的机床主轴轴向变形量与主轴转速呈近似线性关系。主轴轴向变形量随时间的变化趋势符合先快后慢再平稳的自然指数增长形式。
(2)根据数控加工中心主轴的热特性,建立了基于指数函数的热补偿模型。该模型只需主轴转速就可以预报机床的热误差,因此该模型的建模资金成本低、时间短,能够快速应用于工厂环境,而且模型形式简单,易于实施热误差补偿。
(3)在两种不同工况下对该模型的精度进行了验证,结果表明该模型对于预测两种不同工况下的机床主轴热变形量均具有较高的精度。
本文通过分析机床主轴系统的热态特性建立了基于指数函数的热补偿模型。然而除了机床主轴系统外,其他关键零部件的热变形也将对机床的加工精度产生影响。因此,下一步应进行相关实验和研究,建立能够补偿多个机床零部件热误差的补偿模型。
投稿箱:
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com





