基于Archard 理论的滚珠丝杠磨损预测
2016-11-15 来源:东南大学 沙洲职业工学院 作者:徐向红 汤文成 俞 涛 殷 铭
摘要:在数控机床等自动化设备中,滚珠丝杠副具有相对封闭结构特性。为了研究其磨损特性,基于Archard 模型的增量形式建立了滚珠丝杠副的磨损模型,并通过分析滚珠丝杠副运转过程中的接触变形和接触角的变化,求出接触点的相对速度。考虑到轴向载荷、接触面间的相对速度、离心力和陀螺力矩的影响,推导出滚珠丝杠副磨损后的轴向位移,用数值方法得到了滚珠丝杠副的磨损规律,同时在试验台上进行了实验验证。实验结果表明,在滚珠丝杠副运行中的黏着磨损阶段,磨损模型的理论值与实测值吻合较好, 所建立的滚珠丝杠副磨损模型能够反映黏着磨损阶段的实际磨损变化规律。
关键词:滚珠丝杆副;磨损模型;黏着磨损;磨损预测;Archard
0.引言
滚珠丝杠副在数控机床等自动化设备的系统中起着关键作用,由于滚珠与丝杠和螺母之间都是紧密接触并有相对运动,运行中必然会导致磨损,使整个系统振动加大、精度降低。由于磨损现象复杂多样,很难准确预测滚珠丝杠副的寿命,而试验探索的代价较高,结果也不尽如人意。高速精密滚珠丝杠副的磨损问题已经成为国内急需解决的关键技术,严重制约了相关行业的发展,目前对于滚珠丝杠副的研究重点集中在运动学和动力学特征行为,而对摩擦磨损的研究还不深入,迫切需要加强这方面的研究,以提高国内精密数控机床的性能。
滚珠丝杠副中的磨损主要源自滚珠与丝杠和螺母滚道的滑动摩擦[1] 。由于滚道表面不同位置的线速度与到丝杠轴线的距离成正比,且滚珠在绕丝杠轴线旋转的同时还相对接触面的法线自转,因此滚珠与丝杠和螺母滚道表面的接触点上的线速度不可能完全相等,滚珠与滚道必然会产生相对滑动。由于滚珠丝杠副是个相对封闭的装置,在工作中很难直接观测内部参数的变化,必须借助运动学分析获得相关参数,进而建立滚珠丝杠副的磨损与载荷、接触面相对速度之间的关系[2-3] 。
滚珠丝杠装置受力后产生的弹性变形会降低其动态传动精度,陈勇将等人[1] 分析了微型滚珠丝杠副的摩擦机理,建立了微型滚珠丝杠副的摩擦力矩模型;Amin Kamalzadeh 等人[4] 依据动力学模型分析了弹性变形引起的行程误差并建立了相关仿真模型;吴保群等人[5] 基于摩擦学理论建立了滚珠丝杠副摩擦系数与载荷、磨损率与载荷的简化计算公式;Jui-Pin Hung 等人[6] 基于有限元分析法对滚珠与返向器之间的冲击失效过程进行了分析与仿真;Chin ChungWei 等人[7] 分析了预载荷和润滑条件对滚珠丝杠副摩擦力与机械效率的影响;Christian Brecher 等人[8] 研究了润滑条件对滚珠丝杠副磨损过程和摩擦力的影响关系;A. Verl 等人[9] 研究了预紧力对滚珠丝杠副工作时的等效载荷与寿命的影响关系;Horng 等人[10] 建立了不同颗粒变形下的三体微接触模型。
在磨损研究方面,Xiulin Sui 等人[11] 建立了球形端铣刀磨损数学模型以预测在铣削过程中刀具的磨损量;张详坡等人[12] 采用组合磨损计算方法分别建立了自润滑推力关节轴承和向心关节轴承的磨损寿命模型;钟洋等人[13] 运用Archard 磨损理论分析了滚珠直线导轨副的磨损过程并建立滑块位移的计算模型,用来预测滚珠直线导轨副的磨损量;Weijun Tao 等人[14]借助Archard 磨损理论分析了滚柱直线导轨的磨损过程;Xuejin Shen 等人[15] 基于Archard 磨损模型模拟了滑动轴承的非线性磨损过程;Mirbagheri,S. E 等人[16]建立了光盘驱动步进电机的轴承磨损模型,并用试验结果确定轴承磨损模型的常数;Chin-Chung Wei 等人[17] 研究了滚珠丝杠副的预载荷对滚道接触面微凸体磨损率与接触面相对速度、工作行程关系的影响。
上述研究在高速精密滚珠丝杠副力学特性与磨损关系方面还不成熟,有关研究成果较少并不够完整。本文基于Archard 模型的增量形式,分析了滚珠丝杠副运转过程中的接触变形和接触角的变化,同时考虑了轴向载荷、离心力和陀螺力矩的作用,建立了滚珠磨损模型,并用数值方法求出滚珠丝杠副的磨损规律。
1.理论分析
1. 1 滚珠与滚道接触的磨损模型
滚珠丝杠副的磨损是个动态过程,涉及诸多参数。基于黏着磨损机理,根据Archard 提出的近似计算公式可以估算滚珠丝杠副的磨损量:
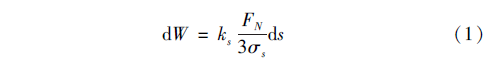

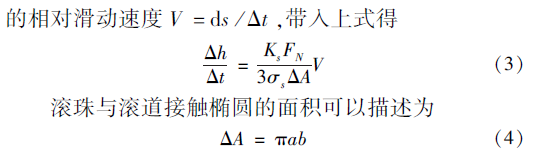
式中,椭圆参数a 和b 分别为接触区域投影椭圆的长半轴和短半轴。
设Fa 为施加于滚珠丝杆副螺母上轴向力Fa ,则根据几何关系有

式(6)为滚珠与滚道接触的磨损模型。下面结合Hertz 弹性接触特性和运动学分析求解滚珠与丝杠滚道、滚珠与螺母滚道接触点的变形、接触角和相对滑动速度。
1. 2 接触面的变形
根据Hertz 弹性接触理论,两物体接触点在法向力FN 作用下产生的接触椭圆尺寸及接触变形为[19] :

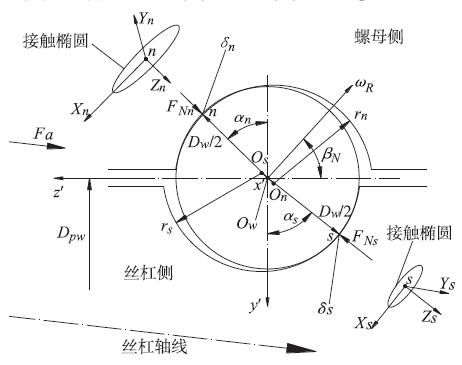
图1 滚珠与滚道接触示意图

丝杠滚道表面与滚珠接触点的两个主曲率分别为:
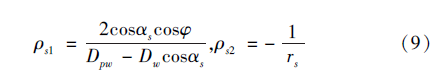
螺母滚道表面与滚珠接触点的两个主曲率分别为:
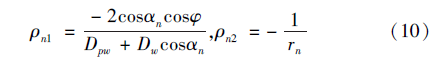
滚珠与丝杠及螺母滚道接触点的曲率和分别为:
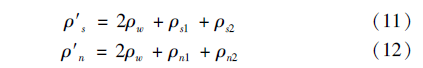

在滚珠与螺母接触处:

1. 3 加载时接触角的变化
滚珠高速旋转时受到离心力和陀螺力矩作用,滚珠中心、丝杠和螺母滚道曲率中心的相对位置也会发生变化,使得滚珠与丝杠滚道、滚珠与螺母滚道的接触角发生改变。
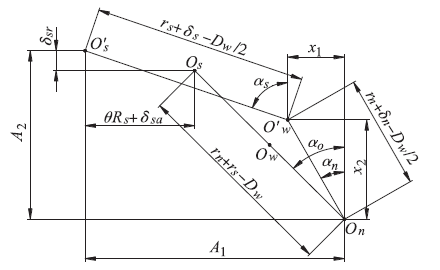
图2 滚珠中心和滚道曲率中心的位置


根据几何关系,可以得到:
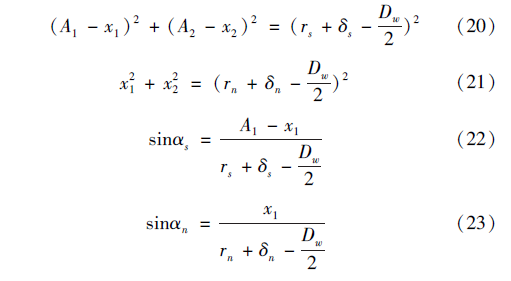

1. 4 滚珠的力平衡方程
滚珠旋转时受到的接触点法向力、摩擦力以及离心力等近似在一个平面内,如果忽略其它方向很小的摩擦力,则如图3 所示。其中钢制滚珠旋转时产生的离心力

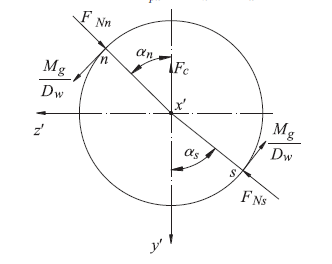
图3 滚珠受力示意图


式中, K 为滚珠与丝杠和螺母之间的接触刚度系数,可由结构参数计算求出
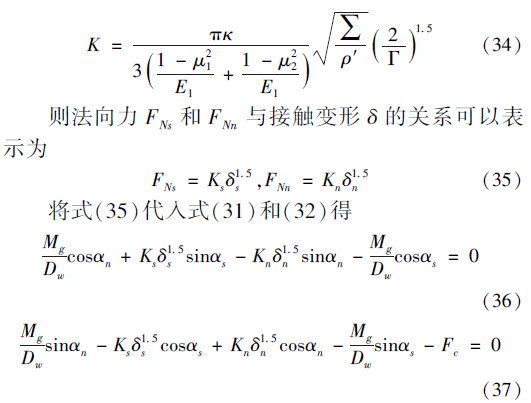


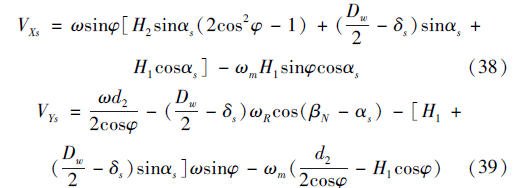
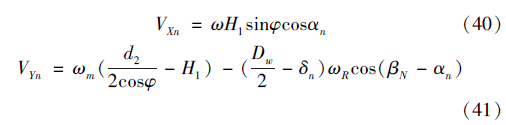

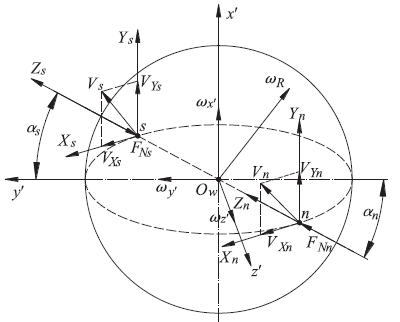
图4 滚珠与丝杠和螺母接触点的相对滑动速度
1. 6 磨损的理论计算




则滚珠丝杆副运行后螺母相对于丝杠的轴向位移为
2.实验验证
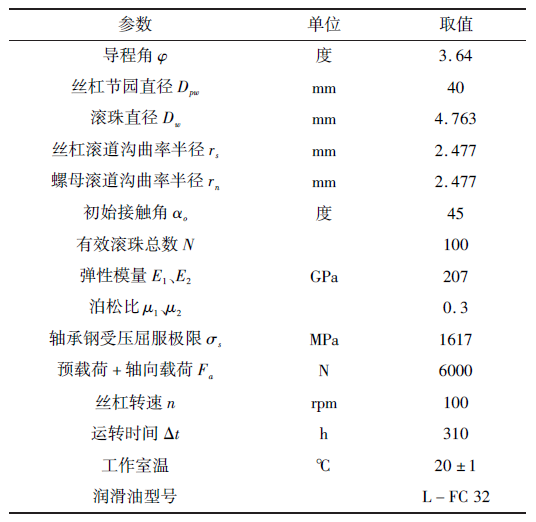
下面根据上述模型以某一型号滚珠丝杆副为例进行理论计算与试验对比,其结构参数和运行工况条件如表1 所示。为了得到理想的载荷状态,本试验在自上而下的立式结构试验台上进行,借助施加在试验台下方的配重块模拟轴向载荷的施加[20]
表1 滚珠丝杠副结构参数和运行工况
在磨损试验的前期,新的样件处于磨合期,试验测量值起伏变化较大。在试验时,先将用于测试的滚珠丝杠副磨合50h,使其进入稳定运行状态;然后,选取磨合后的稳定运行阶段的磨损量进行模型计算与试验对比分析,并在50 ~300h 的时间段内每隔50h 测量一次有效行程变动量,用有效行程变动量表示滚珠丝杆误差和测量偏差的干扰,试验采用三根滚珠丝杠副按同一工况条件运行后取平均值。我们将试验运行到第50h 的有效行程变动量测量值作为初始磨损量基准值,则此后各阶段的有效行程变动量测量值与基准值之差就是相对磨损量的测量值,得到磨损量随时间的变化规律如表2 所示结果。图5 为滚珠丝杠副磨损量的实测值与理论计算值对比图,从中可以看出,在本次试验的50 ~300h 阶段内,滚珠丝杠副磨损量的实测值与理论计算值的变化趋势基本一致,当试验时间大于300h 后磨损量的实测值明显增大。
表2 滚珠丝杠副磨损量的实测值与理论计算值
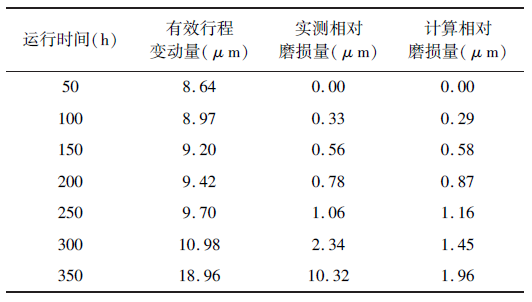
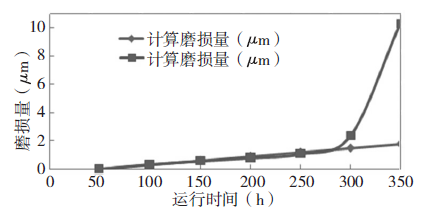
图5 滚珠丝杠副磨损量的实测值与理论计算值对比
由于本文的理论模型是根据黏着磨损机理建立的,试验证明,计算的磨损理论值与实测值在黏着磨损阶段吻合较好,表明磨损模型准确可靠。试验也表明,在滚珠丝杠副工作初期,发生黏着磨损的可能性较大;随着磨损发展,磨损过程中剥落的磨屑与表面的相对运动又会加剧滚珠丝杠副的磨损,使滚珠丝杠副磨损量明显增大。
3.结论
本文在滚珠与丝杠和螺母接触点的变形分析的基础上,考虑了加载时接触角的变化和接触点的相对滑动速度的影响,基于黏着磨损机理建立了滚珠丝杠副的磨损模型,推导出磨损后螺母相对丝杠的轴向位移。对比试验的实测值较好地验证了理论模型的计算结果,所建立的滚珠丝杠副磨损模型能够反映黏着磨损阶段的实际磨损变化规律。在滚珠丝杠副工作初期主要发生黏着磨损,随着磨损发展,剥落的磨屑会诱发磨料磨损,加剧滚珠丝杠的磨损。
投稿箱:
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com





