盾构机刀具失效性的仿真分析
2020-4-7 来源:南京农业大学工学院 作者:何佳闻
摘要: 本文以某地铁线盾构机挖掘过程中失效的刀具为依据,建立了三维刀具切割模型,并进行力学分析,推导出内侧力理论公式,并验证了有效性。同时,分析了刀环侧向力的影响因素,探讨了内侧力与刀盘断裂之间的相关性,据此优化盘式刀具的间距和工作盾构隧道参数。
关键词: 盾构机; 刀具; 失效性; 仿真分析
盾构机(Shield Tunnel Boring Machine)是工程机械装备制造业的标志性产品,也是当今世界上最先进的地下工程与隧道掘进超大型专用设备,具有开挖切削土体、输送土碴、拼装隧道衬砌、测量导向纠偏等功能[1]。目前随着工业化技术的进程以及智能化的发展,限制盾构机发展制造的主要因素有盾构机的速度,切割头的扭矩,构机千斤顶的推力向前移动,其效率与切割室内压力的稳定性、从切割室中取出泥土的数量和质量等有关。同样这些因素也严重影响了盾构机的使用,造成了刀具的失效等[2]。鉴于此,开展盾构机刀具失效过程的力学分析与影响因素探究非常必要。以某地铁线盾构机挖掘过程中刀具失效为工程背景,对其失效过程、影响因素进行了深入分析与探讨。
1、 工程应用方案
针对某城市地铁隧道盾构机挖掘过程中钎焊材料刀具的失效性分析。在该地区,岩石的无侧限抗压强度(UCS)约为 2.554.4 MPa,而 UCS 在另两种情况约为 70100 MPa[3,4]。对于较软的岩石,圆盘切割机深入岩石,意味着接触切割环与岩石之间的面积比较大。对于坚硬的岩石,穿透深度较浅,接触面积较大相对较小。因此,切割环上的正常冲击载荷是主要的。另一方面,刀环的材质是由硬质合金制成,能够承受高正常冲击载荷但易受侧向载荷。因此,这是合理的将切割环断裂归因于切割环上的侧向力。
2 、数据模拟
2.1 模型设计
图 1 显示了刀具环切的三维(3-D)模型设计图,其中(a)总体图,(b)切割刀具环,(c)切割刀具主体。
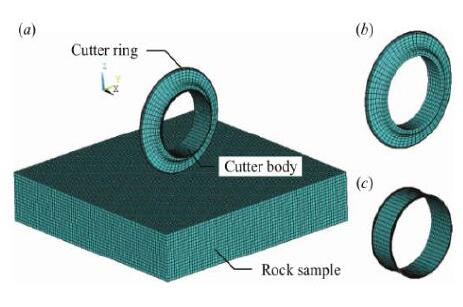
图1 三维刀具
2.2 数值模拟参数
LS-DYNA 是一种用于大变形动力学的显式有限元求解器复杂的影响问题,这里用作数值工具。如图 1 所示,使用的仿真模型包括三部分:岩石样本,切割器环和切割器本体用于控制切割器环的运动。盘片切割机(432 mm),横截面为恒定(CCS),尺寸如图 2 所示。关于岩石样本,除了可自由变形的顶部边界之外,所有其他边界在位移和旋转中都是固定的。此外,采用非反射边界条件来减轻由反射引起的意外故障波浪。数值模型中岩样和刀具材料模型均采用*MAT_CONCRETE,岩样尺寸为 1.0 m×1.0 m×0.2 m,其模型节点数量 150000,元素数量 102400。刀具密度取 8930 kg/m3,泊松比 0.33。
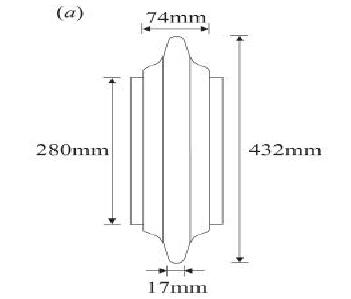
图 2 模型尺寸参数示意图
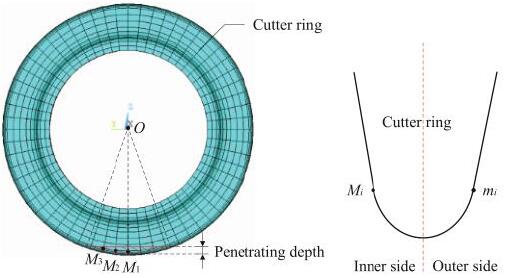
图 3 侧向力的影响区域和监测点的位置示意图
使用替代方法,因为难以直接测量切割环上的侧向力。三次监测选择刀环内侧的点(M1-3),如图 3 所示,以测量表面应力。平均值受监测的表面应力被用来表示内侧力。另外三个监测点(13 m)在外侧用刀环来揭示侧向力的差异,其中 Mi 表示内部测量点,mi 表示外部测量点。圆形切割过程之前的时间间隔用于释放由初始引起的岩石样品中的应力渗透。由于圆形切割过程中正常表面应力发生变化,记录应力的时间间隔为 a 对监测值有明显的影响。在 0.0025 s 的时间步长内,圆形切割的路径长度(d=1.5 m,r=216 mm,ω=1.0 rad/s)约为 0.0375 m,盘刀的滚动角度约为 9.9°。根据滚动角度,所有三个内侧的监测点一直处于横向剪切的影响区域。所以三者的平均值监测点可以用来表示内切割环上的表面应力的总体水平。
3 、仿真结果分析
3.1 失效过程的力学分析
在半径(R)为 0.5 m 的切割过程中(时间步长,T=0.030.05 s),对于初始穿透,岩石的 von-Mises应变轮廓几乎是对称的,这意味着切刀环两侧的侧向力是平衡的。应力分析结果显示,与圆形切割过程一起,与外侧相比,切槽内侧的应变越来越大。在这段时间,圆盘切割机开始圆形切割过程。图 4 显示了中央区域和外部区域岩石的应变轮廓的差异。对于间距半径为 2.0 m 的圆盘切割机,切割槽内外边缘的 von-Mises 应变轮廓几乎是对称的,如图 4(b)所示。虽然中心区域的冯米塞斯应变轮廓不对称,内部应变很大如图 4(a)所示,高于环外的应变。这一现象表明,侧剪力是一个主要问题中部地区岩石破坏的原因,而在外部地区正常影响是主要原因。其中,模拟参数条件(a)T=0.04 s,R=0.5 m; (b) T=0.04 s,R=2.0 m。
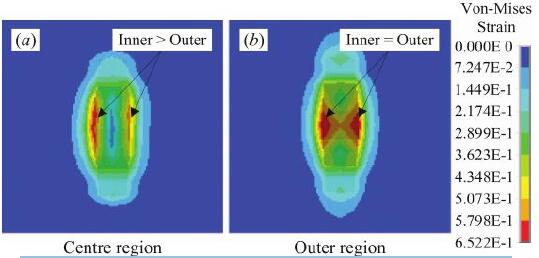
图 4 中央区域和外部区域岩石的应变轮廓的差异示意图
图 5 显示了在不同的间距半径(R)值下刀盘内侧力和外侧力的比值。图 5 中“1”线以上的结果表明内侧力大于圆形期间的外侧力切割过程。通常,如图 5 所示,小间隔半径处的比例大于大间隔半径处的比例。此外,盘刀在切割中的滚动运动槽使监测点的位置也发生变化,导致比例值的波动。
当圆形切割开始时,监测点 Mi 和 mi 立即离开侧向剪切区域,以便监测结果显示一个挥动的曲线。
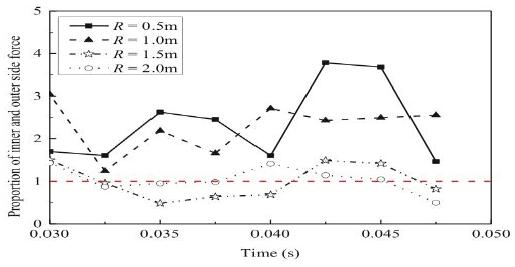
图 5 不同间距半径的切割过程中的侧向力的比例
3.2 内侧力的理论公式推导
作用在切割环上的内侧力也可以通过积分面积(S)上的表面应力来计算:

其中σx 是切割环上的法向表面应力,S 是切割环上内侧力的影响区域。由于内侧力的影响区域较小,可以用监测的表面应力的平均值来表示近似力(Fi)。因此,可以推导为:

σx 是切割环接触面上的平均表面应力,σxi 是监测点 Mi 的法向表面应力,n 是监测点总数以及监测点数量。
根据公式(2)和数值结果,可以计算内侧力以及推断出影响因子 f(ω),见图 6。影响因子点的波动可能归因于岩石样品的脆性破坏和动态切割过程。通过回归分析,影响因子可以很好地匹配指数函数(f(ω)=exp(1.26-0.50ω+0.08ω2)。影响因子随着角速度的增加而下降,因为正常的冲击变得更强,角速度很高,并导致岩石中的主要岩石破坏切槽,受侧向力剪切的岩石变小,侧向力影响因子减少。
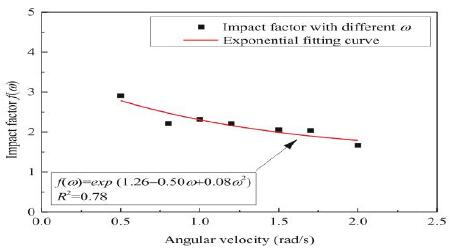
图 6 影响因子和角速度之间的相关性
这个半理论方程(即,f(ω)=exp(1.26-0.50ω+0.08ω2)取岩石的剪切强度,盘刀的尺寸和位置,穿透深度,以及考虑到切割头旋转的角速度。
3.2 影响侧向力的因素
为了验证数值结果,引入了另一种计算侧向力的方法[5]。张建熙提出的方法[6]基于静态应力分析。动态效应和圆形切割过程使得数值结果大于计算值,如图 7 所示。图 7 还显示了具有不同角速度的内侧力的数值和半理论结果。半理论结果与数值结果具有良好的一致性。随着内侧力增加而角速度减小,这与图 6 中观察到的现象类似。当正常冲击变得更强,角速度更高,会导致切削中的主要岩石破坏,内侧力数值减少。
图 8 显示了不同穿透深度的数值和半理论结果的比较。比较显示半理论结果可以很好地匹配数值结果,特别是在较小的穿透深度。当穿透深度增加,从数值方法获得的内侧力增加的速度比通过半数值法计算的更快,理论方程造成这种差异的原因可能是由于侧向力只引起剪切的假设切割槽中的岩石失效。然而,随着穿透深度的增加,岩石的破碎类型逐渐增加从剪切失败变为压缩失败。由于岩石的抗压强度远大于剪切强度,随着穿透深度的增加,数值模拟的内侧力增长更快。
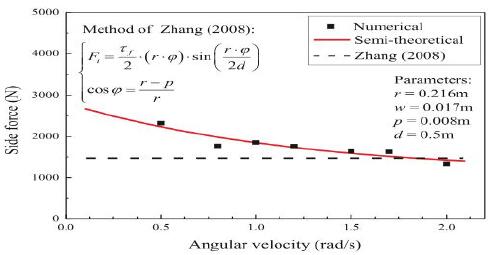
图 7 数值和半理论结果与不同角速度的比较
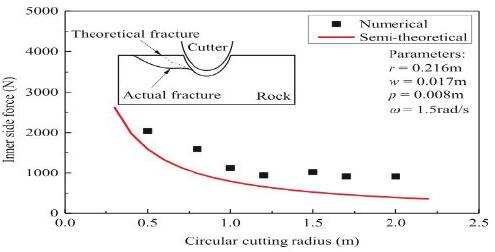
图 8 数值和半理论结果与不同圆形切削半径的比较
3.3 内侧力与刀盘断裂之间的相关性
使用公式(2)中,可以计算圆形切削过程中刀环上的内侧力。图 9 比较了侧面力和相应的切割环断裂的累计百分比。尽管侧向力急剧下降,在切割头的中心区域的平均侧向力高。因此,内部区域中刀片断裂的风险较高。但是,刀圈断裂的增加率(曲线的斜率代表累积百分比)差不多稳定而内侧力急剧下降。原因在于数值中使用的盘形刀的间距半径的范围模拟为 0.52.0 m。因此,超出范围的刀架中心附近的计算结果可能不正确。在外部区域,侧向力低于 1000 N 的线(缓慢减小),因此很少发生切割环断裂。该对比结果表明,刀圈断裂的高风险与内侧力的高水平相关。在这种情况下 8 mm 的穿透深度(即 d/0.5D=0.18),平均法向表面应力(σx)将大于 3.2 MPa(σx=Fi/S)当内侧力达到 1000 N 时。因此,小于 1000 N 的侧向力可以被认为是安全值防止刀圈断裂。
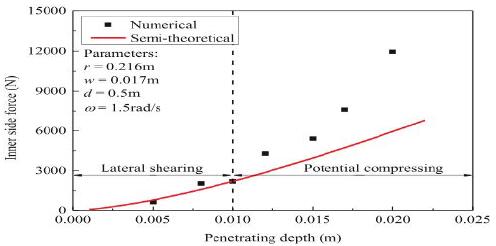
图 9 刀具环断裂和内侧力的相关性
4、 结 论
本章主要基于某地区地铁隧道挖掘过程中盾构机的刀具失效情况进行模拟分析。通过总结刀环断裂的特点,我们认为刀环的失效可以与内环相关联侧力。通过力学分析和数值模拟,可以计算出刀环的侧向力和影响的影响讨论因素。对刀盘断裂的失效分析可以用来优化盘式刀具的间距和工作盾构隧道参数。更具体的结论如下:
(1)根据工程案例收集到的现场数据,更容易发生刀具断裂中心区域而不是外部区域;
(2)提出了考虑岩石和隧道抗剪强度的内侧力半理论计算公式参数。通过将半理论结果与数值结果进行比较来验证该公式,具有很好的一致性。
投稿箱:
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
更多相关信息




