面向能效的曲面数控加工刀具路径优化方法(下)
2018-10-8 来源:西南大学工程技术学院 作者: 李 丽 邓兴国 尚川博
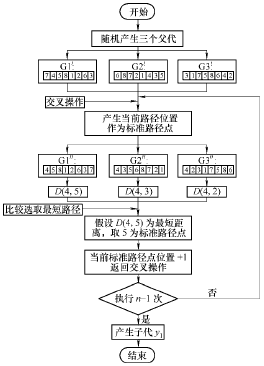
图 4 子代 y1产生过程图
由贪心三父代算法设计的交叉算子可得出,产生的两个子代都较好地遗传 3 个父代的两方向的基因,每次选择的都是 3 个父代中最好的基因,使得后代完全继承了父代全部优秀的基因,产生更加优秀的子代。通过对交叉算子的改进,使得寻优搜索效率变高,同时提高了全局寻优能力,缩短了寻优时间。
(3)自适应模拟退火和精英混合选择策略。 经过上述交叉变异后生成的两个子代,但并未直接用新生成的子代代替原有三个父代,而是在此五个中选择最优的三个作为下一轮的父代。通常遗传算法采用轮盘赌选择方式,该方式在群体规模较小时能够很好地选择出优秀的个体,群体规模一旦过大,该选择方式无异于随机选择。本文利用自适应模拟退火算法与精英混合的选择策略,过程如下所述。
(1) 计算交叉操作的三个父代适应度分别为F(G1)、F(G2)、F(G3)。
(2) 再计算产生的两个子代的适应度 F(y1)、F (y2):① 如果 F(y1)≤F(y2),则子代 y1被接受进新种群,否则 y1以概率 exp[(−F(y1)−F(y2)/T]被接受(T 为控制参数);② 在进化初期,T 值较大,适应度差的子代有更大的概率被接受,以保证前期种群的多样性,随着迭代的进行,T 逐渐减小,适应度差的个体的接受概率逐渐减低,避免破坏种群的适应度。 (3) 为加快种群前期的收敛速度,算法中同时引入精英选择方法,即直接将适应度最大、数量为k 个的个体替换最小适应度和数量相同的个体。
3.2.4 循环模式的改进
基本遗传算法的循环模式比较单一,通过设定最大迭代次数来进行遗传操作,当迭代次数达到最大值即停止遗传操作,使得收敛速度过快,容易陷入局部最优解。通过引入自适应模拟退火算法的思想,将模拟退火算法中的温度参数转变为控制参数。当种群收敛时,而未获得最优解,则可进行参数调整后继续计算,以寻求得到最优刀具路径。过程如下所述。
参数设定:控制参数初始值 T0、控制参数初始值的衰减函数 w、停止参数 Tf等。
while 1 {选择、交叉、变异} 当前代数+1,当前控制参数 T0=T0*w 判断当前种群中最好个体的适应值是否小于父代种群中最好个体,如果连续 5 代小于父代种群中最好个体的适应值,则结束循环,或者当前温度T0<Tf也结束循环。否则,继续交叉、变异和选择操作。end
4、实例及验证
4.1 试验条件
试验设备:济南第三机床公司的 JTVC650B 立式加工中心,日置 PW6001 功率分析仪来监测机床切削过程的实时功率。
工件材料及加工要求:工件材料为 C6061 铝合金棒,直径 d=36 mm,半精加工深度 ap=0.5 mm,加工表面粗糙度 Ra不超过 6.4 μm。刀具:材料为硬质合金球头铣刀,粗加工刀具直径 R=5 mm。
4.2 刀触点优化结果
图 5a 为建立的曲面模型,模型直径 d=36 mm。图 5b 为曲率分析图,可得曲面凹处最大法曲率 kmax = 0.36,待加工曲面表面粗糙度要求为不超过
6.4 μm,由前面的描述得半精加工时球头铣刀的半径取R=2.5 mm,则由式(21)得 l=0.73 mm。按照等参数线采样法对曲面进行离散,离散结果如图 5c 所示。最后得到合理的控制点共 2 075 个,即刀触点数和初始种群数为 2 075 个,如图 5d 所示。
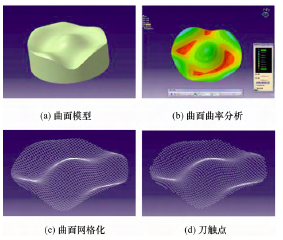
图 5 刀触点优化过程
4.3 刀具路径优化结果
采用 Matlab 进行传统遗传算法和自适应模拟退火遗传算法的刀具路径寻优计算。参数设置为:基本遗传算法:种群大小 S=3 000,迭代次数 c=450,交叉概率 Pc=0.9、Pm=0.1。改进遗传算法:种群规模 S=3 000,迭代次数 c=450,交叉概率 Pc1=0.95、Pc2=0.7,变异概率 Pm1=0.5、Pm2=0.2,选择复制个数 w=50;控制参数初始值 T0=5 000,衰减函数k=0.95,停止参数 Tf。基本遗传算法在计算中出现了早熟收敛的情况,而改进遗传迭代次数为260 次,得到刀具路径最优长度 L=1 548.52 mm。图6 分别为改进遗传算法的刀具路径图、投影图及与计算过程收敛情况图,其中图 6a 表示经自适应模拟退火遗传算法计算后产生的最优化刀具路径图,图 6b为刀具路径图在 XY 平面上的投影图,图 6c 为自适应模拟退火遗传算法计算最优刀具路径的收敛过程图。
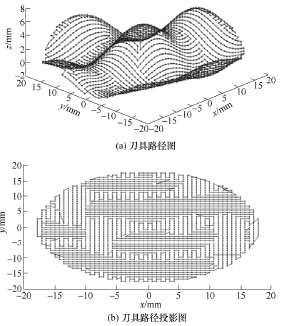
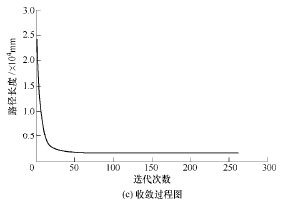
图 6 刀具路径、投影图以及计算过程收敛情况
4.4 仿真结果分析
曲面模型加工的切削仿真路径在 Master CAM数控编程软件中进行,根据本文建立的曲面特点,选择平行铣削、45°平行铣削和流线型铣削生成半精加工刀具路径作为仿真对比,粗加工则采用相同的等高轮廓铣削方式,以最快速度去除材料,刀具半径为 5 mm,加工余量均留为 0.5 mm;本文研究的重点在半精加工阶段,半精加工参数设置为:刀具半径为 2.5 mm;切削用量:每齿进给量 fz=0.03 mm/z ,主轴转速 n=3 500 r/min ,进给量 f=400 mm/min。
根据本文提出的刀具路径生成方法,并通过Matlab 求解得到了最优刀具路径,并在 Master CAM数控编程软件中通过设置相应加工参数,仿真模拟得到了如图 7 所示生成的不同刀具路径。表 1 为对应刀具路径下仿真模拟得到的刀具路径长度以及切削时间。
从图 7 可看出,在保证加工质量的前提下,本文提出的算法生成的曲面加工刀具路径规划完全可行且连续性非常好,相对目前常用的路径生成方法而言,超出工件加工面的空切行程路径较少。
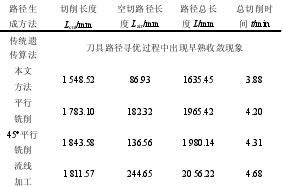
表 1 各方法生成的刀具路径比较
由表 1 得出,本文方法生成的刀具路径无论是切削长度还是空切路径长度都有明显的优势。切削长度最大优化距离为 295.06 mm,相对减少 16.00%,最短优化距离为 234.58 mm,相对减少 13.16%;路径总长度方面,可看出本文方法计算出的刀具路径优势更加明显,刀具路径总长度最大优化长度达到420.77 mm,相对减少 20.46%,最短优化长度为329.97 mm,相对减少 16.79%;
从表 1 数据可知,当其他参数一定时,刀具路径的长度直接决定了机床的加工效率,刀具路径的优化影响着总切削时间,刀具路径长度减少,使得总切削时间变短,进而提高加工效率,验证了面向刀具路径优化的加工效率函数的正确性。
4.5 试验验证
将构建的曲面模型与生成的刀具路径在其他外部环境以及切削参数设置相同条件下进行实际加工,且每种不同的加工方式分别进行了 5 次试验,并记录每次加工过程中的功率消耗值,取平均值作为最后的能耗值,模型曲面加工试验结果如图 8 所示,每种加工方法的实测 Pcut和 Pair功率值分别如表 2 和表 3 所示。
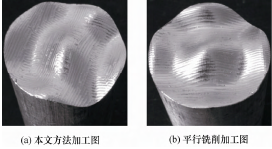
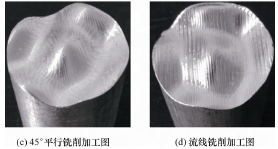
图 8 实际加工结果
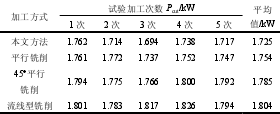
表 2 各路径实际加工实测切削功率 Pcut
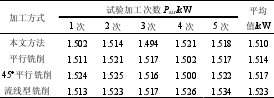
表 3 各路径实际加工实测空切功率 Pair
由表 2、3 可看出,在进行实际加工时,本文提出的路径优化算法生成的刀具路径,机床消耗的功率较少。又因刀具路径长度的减少,使得加工时间变短,从而整个加工能耗最小,表 4 为各路径加工方式下的能耗值大小,从表中得出运用该刀具路径优化方法进行零件加工时,机床所消耗的能耗相对于其他加工方法最低减少了 8.94%,最高减少了20.57%。进而验证了面向刀具路径优化的机床能耗函数的正确性。
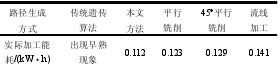
表 4 各路径加工机床能耗对比
5、结论
(1) 分析了刀具路径对加工效率和刀具路径对机床能耗间的映射关系,建立了以机床能耗和加工效率为目标,以机床主轴转速、进给量、最大切削功率、最大切削力、加工行距等为约束的刀具路径优化数学模型。
(2) 提出了一种刀触点优化方法,该方法根据进刀方向法曲率半径、刀具半径以及曲面加工后残留高度,把待加工的曲面进行自适应离散,从而得到曲面控制点,以各个控制点作为刀具加工路径的刀触点。
(3) 提出了一种自适应模拟退火遗传算法进行刀具路径刀触点连接顺序及方式优化方法,该方法引入模拟退火算法、贪心算法对遗传算子进行了改进,提高了算法在进行大量曲面控制点计算寻求最优路径时种群进化速度,避免陷入局部最优解,加快了运算速度。 但是由于数控加工方式种类多,本文主要针对曲面模型半精加工单工序为高效低耗刀具路径优化研究,而实际曲面零件加工是一个多工序、多加工方式的过程,且同一个曲面零件加工可以由多条工艺路线完成,因此,从曲面零件多工序、多工艺路线上进行刀具路径优化,进而降低机床能耗将是以后研究的重点。
投稿箱:
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com




