曲面综合法弧齿锥齿轮加工参数计算
2016-9-13 来源:河南科技大学机电工程学院 作者:魏冰阳 邓效忠 仝昂鑫 杨建军
摘要:针对现有弧齿锥齿轮加工参数计算方法,接触点综合纷繁复杂的问题,提出ease.off曲面综合法。从微分几何学出发,给出二阶密切曲面的定义及其构造方法;在二阶精度范围内,密切曲面与原有曲面具有相同的微分几何属性,从而可以替代原有的曲面分析。通过弧齿锥齿轮加工的产成模型,构造大小轮共轭齿面的ease.off差齿面,利用ease.off差齿面的密切曲面完整地拓扑齿面接触区;利用齿面接触区的可控参数综合确定小轮齿面的接触参数,进而通过数值优化方法求解小轮的加工参数。籍助ease-off密切曲面进行了啮合仿真,完整呈现了齿面接触区大小形状、接触路径方向、抛物线失切量等轮齿啮合信息。所提出的方法适宜于数值方法,基于齿面接触区的完整性,实现了齿面啮合性能较好控制。
关键词:二次曲面;轮齿接触分析:弧齿锥齿轮;差齿面
0前言
弧齿锥齿轮在机械动力传输领域具有广泛的应用,其啮合理论和制造技术一直是各国专家学者研究的热点。20世纪90年代起,随着计算机数值计算方法的应用,弧齿锥齿轮啮合性能预控理论和设计技术得到快速的发展。LITIVIN等[1-3]发展了“局部综合”法,预置在参考点二阶接触参数,以期对轮齿传动误差和齿面印痕进行控制。吴训成等[4-6]发展了“主动设计”,通过预置传动规律,接触线方向修形,达到对齿面的啮合性能预控的目的。周凯红等[7-8]发展了基于预定啮合特性的点啮合齿面设
计方法。SIMON等[9-10]发展了弧齿锥齿轮加工参数的优化算法。上述方法均是把曲面啮合化为点接触参数,通过接触点参数的综合实现对弧齿锥齿轮接触性能的主动控制。但点接触参数综合在对接触点的矢量、曲率参数计算时,纷繁复杂,多数情况不适合数值方法计算,更不便齿面重构、反求与误差修正技术的应用。
鉴于上述加工参数计算、啮合仿真方法的不足之处,本文拟提出一种曲面综合法,基于齿面接触过程的完整性,通过ease.off差齿面的密切曲面拓扑接触区,实现对齿面接触性能的预控。从微分几何学出发,给出二阶密切曲面的定义及拓扑方法,曲率参数的数值化方法;通过弧齿锥齿轮加工的产成模型,构造ease.off差齿面的密切曲面,通过密切曲面拓扑、接触参数综合确定小轮齿面的接触参数,进而通过数值方法求解小轮的加工参数,最后借助密切曲面完成啮合仿真。
1、二阶密切曲面
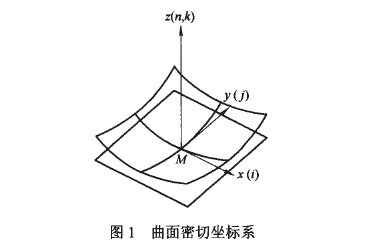
设有一个Σ2类曲面(至少存在2阶以上连续微商),在它上面的一点M处取坐标系(Mxyz),如图1所示,X、Y轴在M点的切平面上,z则在M点的法线刀方向。若曲面Σ2在该坐标系中的方程式为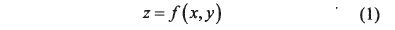
那么,由微分几何学可以知道【ll】,第1I基本形式为
显然这是是一个关于(dx,dy)的二次型。
第1I基本形式近似地等于曲面与切平面的有向距离的两倍,即
由于z轴与M点的法线方向一致,则式(3)表示了z轴的坐标。在小领域内可以用X代替dx,Y代替妙。所以,在M点的邻域可得到如下近似式

式中 ,
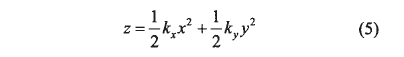
式(4)、(5)表示的曲面Σd和原曲面Σ2在二阶项上是一致的,它们有相同的曲率参数  。因此,把Σd为Σ2的二阶密切曲面。它们在任意方向上都有相同的法曲率及短程挠率。
。因此,把Σd为Σ2的二阶密切曲面。它们在任意方向上都有相同的法曲率及短程挠率。
由于,曲面在正常点的邻域中总可以有式(1)形式的参数表示,所以总存在一张二次曲面形如式(4),而且当且仅当它们具有相同的曲率参数。因此,这一论述可作为微分几何的定理给出:
对于Σ2类曲面在正常点的邻域内,总存在一张与其相切的二次曲面,当且仅当它们具有相同的曲率参数。
由上述分析可以知道,对于Σ2类曲面小邻域内可以由二阶密切曲面代替。本文利用该原理实施弧齿锥齿轮产成曲面的综合、加工参数的计算及分析。
2、弧齿锥齿轮的产成模型
2.1大轮齿面易产成及其方程
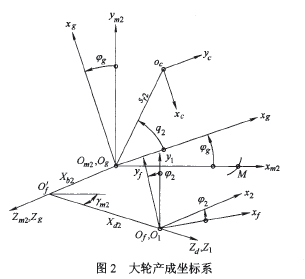
弧齿锥齿轮大轮加工一般采用双面滚切法,加工参数一般有一致的计算方法。用如图2所示的坐标系描述大轮齿面的产成。刀盘坐标系  位于瑶台坐标系
位于瑶台坐标系 第一象限,绕z轴旋转,Sg初始位置与机床坐标系
第一象限,绕z轴旋转,Sg初始位置与机床坐标系 重合,其任意瞬时相对于
重合,其任意瞬时相对于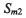 转角
转角 ,则大轮相应的产成转角为
,则大轮相应的产成转角为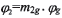 。其余参数
。其余参数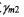 为轮坯安装角(等于大轮根锥角),
为轮坯安装角(等于大轮根锥角),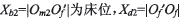 为轴向轮位修正值。根据啮合方程可推得
为轴向轮位修正值。根据啮合方程可推得


2.2共轭小轮齿面Σl
利用大轮齿面产成小轮齿面为包络原理,假设大小轮啮合的初始角度为庇o、咖o,则任意啮合位置大小轮之间的转角的关系为

2.3数值微分求共轭小轮的曲率参数
给定大轮齿面Σ2上参考点 的曲面参数
的曲面参数 ,并给定微分
,并给定微分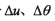 增量,利用上述式(1)~(9)运算,求数值微分
增量,利用上述式(1)~(9)运算,求数值微分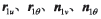 即
即

3 、Ease.off曲面综合
对共轭小轮齿面Σ 1修形,在计算点M领域内必然能够构造一个在M点相切的其余邻域失切的小轮修形齿面,称为切触齿面 ,相应的主方向、主曲率记作
,相应的主方向、主曲率记作
3.1齿面接触区拓扑
在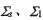 之间沿法线方向构造差曲面称为ease.off曲面
之间沿法线方向构造差曲面称为ease.off曲面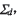 反映了共轭齿面的失切量,该曲面在点M领域可以用形如式(5)的密切曲面代替
反映了共轭齿面的失切量,该曲面在点M领域可以用形如式(5)的密切曲面代替



4、小轮齿面五加工参数的计算
4.1小轮产成模型
根据小轮产成原理,建立如图4所示的坐标系来描述小轮的产成过程。刀盘坐标系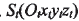
的原点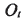 为刀盘中心,
为刀盘中心,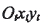 为刀尖平面(与机床平面重合),并与摇台坐标系
为刀尖平面(与机床平面重合),并与摇台坐标系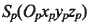
固联,且各坐标轴对应平行。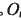 在坐标系SP的极坐(
在坐标系SP的极坐(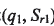 为角向刀位和径向刀位。Sp初始位置与机床坐标系
为角向刀位和径向刀位。Sp初始位置与机床坐标系



4.2小轮加工参数计算与仿真
4.2.1 小轮的ant参数的数值求解
利用前述第2.3节的数值微分方法,对式(20)求数值微分,计算小轮的主方向、主曲率,同时将径矢、法矢统一记作

上述方程是含有小轮加工参数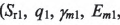
 ,刀盘参数
,刀盘参数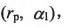 曲纹坐标参数
曲纹坐标参数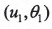
的9个非线性方程组。通过求解该方程组可确定小轮的加工参数。
在求解之前,有些参数是可以首先确定的,轮坯安装角肋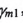 ,刀盘压力角
,刀盘压力角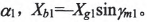
所以实际求解的参数为6个。
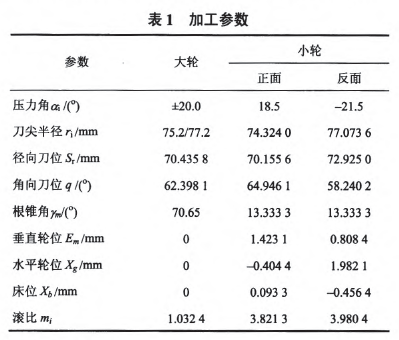
式(22)的解的初值和取值范围是比较容易确定的,所以式(22)适宜用优化的方法求解。本文采用非线性约束优化求解的办法,利用Matlab优化函数fmincon完成了一个实例计算,结果如表1所示。
4.2.2 啮合仿真
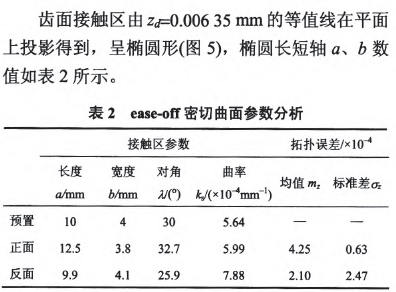
为了验证表l加工参数计算的准确性,通过构建ease—off差齿面进行接触仿真,结果如图5所示ease-off为二次凸曲面,反映齿面接触呈局部共轭特性,齿面两端离差在0.04---0.05 mm之间。通过对
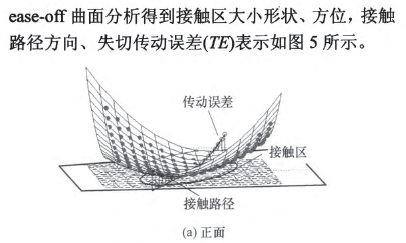
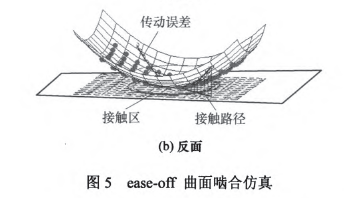

5 、结论
(1)针对现有弧齿锥齿轮N-r参数计算方法,接触点综合纷繁复杂,不适宜数值方法计算的不足之处,给出了ease.off曲面综合法。从微分几何学出发,给出了二阶密切曲面的定义及其拓扑方法;在二阶精度范围内,密切曲面与原有曲面具有相同的微分几何属性,从而可以替代原有的曲面分析。
(2)通过弧齿锥齿轮加工的产成模型,构造了ease—off密切曲面,拓扑齿面接触区;通过曲面综合确定了小轮齿面的接触参数,利用数值方法求解出小轮加工参数,借助ease.off密切曲面完成了齿面的啮合真本文所提出的曲面综合法适合数值计算,能够主控齿面接触区,预置参数能动性较好,啮合仿真呈现了轮齿接触的完整信息。
投稿箱:
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
更多相关信息




