光学自由曲面加工刀具参数选择算法的研究
2020-3-2 来源:天津职业技术师范大学 机械工程学院 作者:聂雅慧
摘 要: 光学自由曲面广泛应用在航空航天、医疗卫生、国防、能源等各个领域。光学自由曲面加工时由于曲面没有型值点限制,且每个位置的曲率各不相同,因此,对加工刀具的选择比较复杂。对光学自由曲面和刀具建立几何模型,通过几何建模分析了刀具与加工点的几何关系。通过数学模型对光学自由曲面加工刀具的前脚、圆弧半径等参数进行选择。为光学自由曲面加工提供了刀具参数选择的理论算法。
关键词: 光学; 自由曲面; 刀具; 参数选择
假设,加工中任意曲面加工时主要考虑坐标原点,z 轴以及加工点构成的平面,如图 1 所示: OZP0,加工时刀具的上表面始终与与 OZP0面重合,因此在对刀具参数的选择时定义加工曲面的参数公式为: Σ: r( u,v) = { x( u,v) ,y( u,v) ,z( u,v) } ,其上任意一点加工点 P0( u0,v0) ,主要考虑曲面 Σ 与 OZP0平面相交所得曲线 Γ 的一系列特征,进而影响刀具参数的选取。首先,对于任意曲面 Σ,根据第一和第二基本齐式,可以写出其曲面的基本量:
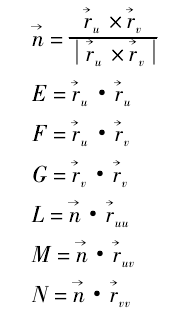
其中,ru表示曲面 Σ 的参数曲线 u 线在点( u,v0) 的切线方向,rv表示曲面 Σ 的参数曲线 u 线在点( u0,v) 的切线方向,ruu= dru/ du,ruv= dru/ dv,rvv= dru/ dv。对于确定的 P0点,其曲面基本量以及法矢量都是确定的并且固定的值,定义这些值分别为 E0,F0,G0,L0,M0,N0,n0。

图 1 刀具加工时的示意图
1 、刀具圆弧半径的选择
曲面 Σ 与加工平面 OZP0相交所得曲线 Γ 在 P0点的切线方向的单位矢量为切矢量 α,在平面中 OZP0中垂直于单位切矢量的单位向量 β,P0点在 OZP0平面上的主法矢为 β,一般称由切矢量及主法矢组成的平面即平面 OZP0为密切面。曲线 Γ 是密切面上的曲线,在加工时,刀具的前刀面也落在密切面上 。
根据默尼埃定理可以计算出密切面中 P0点的曲率:
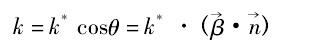
因此,此时圆弧半径 R = 1 /k,对于刀具圆弧半径的要求为刀具圆弧半径小于所计算的 R 值,同时由于刀具的圆弧半径的曲率方向为 OZ 方向,如果曲线为凸曲线,则曲线的法矢量为OZ 的负方向,因此,当 k 值小于 0 时,曲线为凸曲线,对于刀具的圆弧半径没有限制。
2 、扫角的选择
定义矢量 β 与 OZ 的夹角为 γ。考虑到加工方向的变化,为了便于取值,定义 β 与 OZ 之间的夹角始终取锐角。

3、 后脚的选择依据
通过分析,当采用刀具进行加工时,刀具的后角方向是由垂直于刀具前刀面并过加工点的平面内的曲线的方向所决定的。因此,定义一个过 P0点与 OZP0平面垂直并与 z 轴平行的平面定义为 Ψ,定义平面 Ψ 与曲面 Σ 相交所得的曲线为 ΓΨ,该曲线也是一个平面曲线。同样的定义过 P0点曲线 ΓΨ的切线方向的单位矢量为 αΨ,其在密切面内的单位主法矢为 βΨ。
通过分析可以知曲线在 P0点的切线方向与 z 轴之间的夹角决定了刀具的最大后角,因此定义曲线在 P0点的单位切矢αΨ与 z 轴之间的夹角为 γc,则可以计算出:

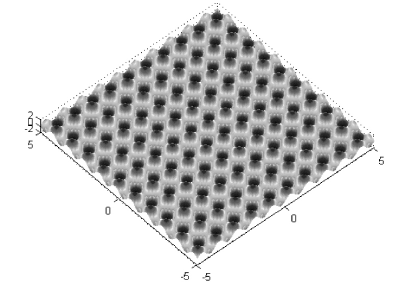
图 2 计算实例: 双正弦曲面
计算后刀具的选择参数为:圆弧半径: R = 0. 02533 mmsweepangle: 83. 5后角: 89. 5与商业化软件分析结果基本相同。
4 、结语
本文以加工光学自由曲面时刀具参数的选择为出发点,分析了光学自由曲面加工时,刀具与所加工的自由曲面之间的几何关系。通过分析自由曲面各面的曲率与刀具参数之间的几何关系,得出了参数选择的数学公式依据。最后,利用软件对自由曲面参数选择进行了仿真实验,所得仿真分析结果与商用软件得出的结果相同。
投稿箱:
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com





