立式加工中心立柱多目标优化设计
2015-12-4 来源: 福州大学研究生院 福建工程学院 作者:杨絮娜 彭晋民
摘要: 在PROE 和ANSYS Workbench 的平台上建立VL855 加工中心立柱结构的参数化模型,进行Static Structural 和Modal 分析; 通过灵敏度分析选定立柱的壁厚、导轨面凸台厚度、筋板厚度、螺栓槽间距为优化的设计变量,立柱的质量、最大变形、第一阶段振型作为目标变量,进行多目标优化。结果表明: 优化后,立柱质量减少5. 2%,立柱在同样载荷情况下变形量与优化前变形量相近,其低阶模态有所提高,满足工作状态动态要求。
0 前言
在机床等装备结构设计中,通常运用选型法、ANSYS 优化等进行优化解决了较多的工程实际问题。仇君等人 通过分析立柱不同加载方式,运用力学理论知识采用选型法对钻床立柱结构设计进行优化; 盛艳君等根据CK516 数控车床的立柱的动静态分析结果确定需要改变立柱的壁厚来达到减重的目的; 以上都是基于经验和判断做出结构的改变方案,必要时则需要多次的设计方案修改。Dezhong 等 ]数控利用FEA 钻床的关键部件立柱结构以减轻质量为优化优化目标进行尺寸和拓扑优化,使立柱的质量减少了7. 36%,但无法同时实现减少立柱的受力变形或提高振动频率。本文作者通过ANSYS Workbench 应用立柱模型参数与响应面法[4]实现关于立柱质量m、静力变形δ 及第一阶模态f 为多目标的n 个结构设计变量的函数表达式,形成n 维空间曲面,从而通过目标优化驱动,得到最优解。
1 、立柱结构分析与建模
1. 1 立柱结构三维模型的确定
如图1 所示为立柱简化CAD 模型。建模时忽略了对网格划分十分不利的小特征如倒角、圆角等[4]。根据立柱的结构特点,立柱的壁厚与内部筋板很大程度上决定了立柱动态性,因而主要通过选择立柱的壁厚、内部筋来进行立柱的优化。
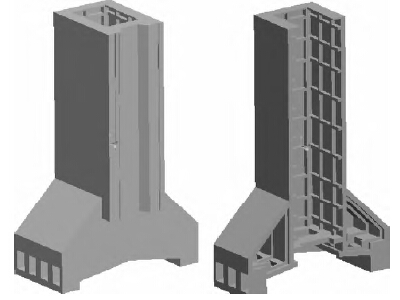
图1 立柱CAD 模型
1. 2 立柱的动态特性分析
1. 2. 1 加工中心立柱载荷分析
1. 2. 1. 1 立柱的力学模型分析
加工中心立柱所受的加工载荷是通过主轴箱传递的,其力学模型如图2 所示。
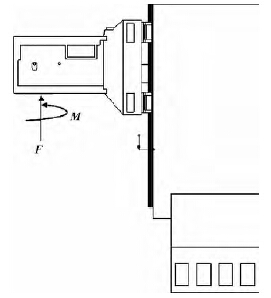
图2 立柱结构的力学模型
加工中心在钻削时的钻削力和钻削扭转计算公式 :



图3 立柱结构网格划分
对该模型加载分析,得到立柱的变形图,如图4所示。
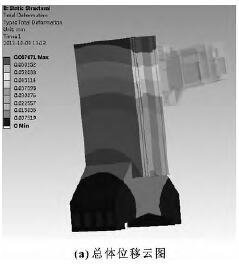
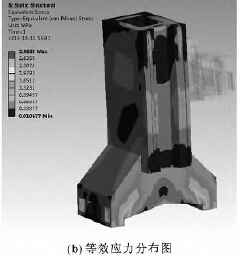
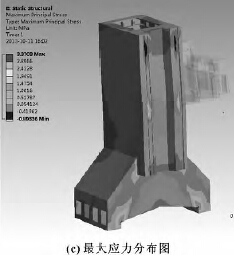
图4 立柱加载变形图
由计算结果可知,立柱的总体位移的最大变形变形值为0. 067 671 mm,发生在立柱的前壁上端; 立柱的结构的刚性影响整机加工精度,主要是反映在导轨面的变形,特别是与主轴箱所在位置,总体来看,主轴箱所在位置的导轨面变形最大不超过0. 056 mm,这说明该立柱的刚度还是可以满足加工要求。从立柱的应力分布图来看,立柱结构大部分应力在2. 97MPa 以下,最大应力值为3. 37 MPa; 远小于灰铸铁的强度极限300 MPa。
1. 2. 2 加工中心模态分析
在约束状态下,计算出立柱的前六届模态振型图,如图5 所示。


图5 立柱结构振型
VL855 加工中心的主要转速是在0 ~ 4 000 r /min,立柱结构的第一阶模态是72. 801 Hz,略高于机床的主要工作频率范围,其立柱振型的振幅较大出现在立柱上端导轨面,可以通过减小导轨面凸台壁厚来提高立柱的模态。
2 、立柱的结构多目标优化
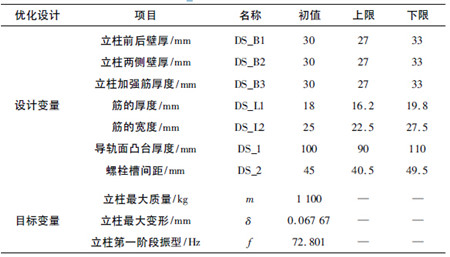
2. 1 优化参数的选择
在保证立柱动态性的同时,对立柱的整体结构进行优化。在立式加工中心钻削载荷中,弯矩是其主要作用载荷,立柱变形形式主要以弯曲变形为主,因此立柱的变形应与截面抗弯惯性矩有关,应可以通过改变立柱的壁厚、导轨面凸台壁厚来优化立柱结构; 先选定立柱的壁厚、导轨面凸台壁厚、筋板厚度、螺栓槽间距为优化的设计变量,将立柱的质量m、最大变形δ、第一阶段振型f 作为目标变量。
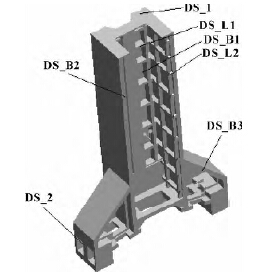
图6 立柱剖面图
在ANSYS Workbench 中DOE ( design of experiments)模块是多目标优化设计的工具[6]。多目标优化设计指建立起多个目标函数,通过数值计算使模型的多项性能指标尽可能地达到最好。与单目标优化设计不同,多目标优化设计的最优解是一个集合,并不是全局的最优解[7]。在Design Exploration 模块中的多目标优化设计D0E 中设置各设计变量及其与立柱其他尺寸参数之间的关系,其优化参数如图6、表1 所示。
表1 立柱优化参数
2. 2 优化参数灵敏度分析
在结构优化设计中,灵敏度分析是分析参数的变化对模型最优解的敏感程度,通过灵敏度分析可以确定参数对模型有多大的影响,去掉影响较小的参数。在立柱结构优化设计中,通过灵敏度分析( 如图7)可得到为各种迭代法实现最优化所需要的设计变量,因此灵敏度分析是任何最优化的重要一步[8]。
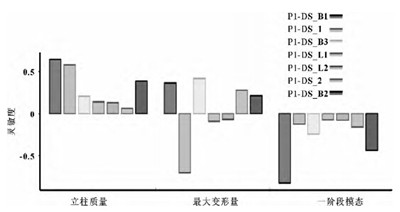
图7 灵敏度分析
2. 3 优化分析与结果
由于立柱优化目标是希望立柱的质量目标函数、最大变形目标函数减小、一阶段模态目标函数增大,因此质量、最大变形目标函数的希望值设置为Minimize,一阶模态目标函数希望值设置为Maximize,但是其主要目标是减轻质量,故立柱的3 个目标函数的优先级不同: 质量为较高等级( Higher) ,最大变形为中间级别( Default) ,振型为较低级别( Lower) 。
2. 3. 1 立柱最大变形目标函数的响应
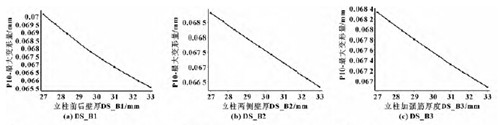
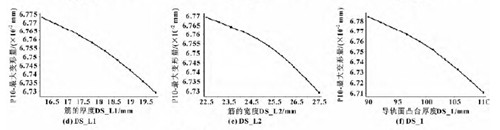
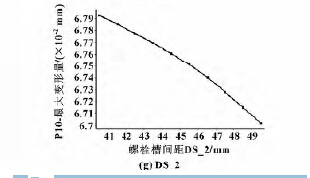
图8 静力最大变形对各个输入参数的响应图
2. 3. 2 立柱一阶模态目标函数的响应
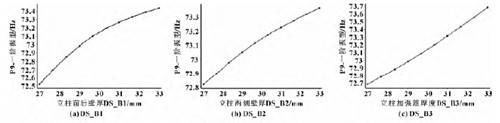
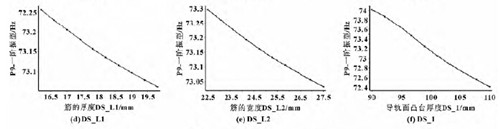
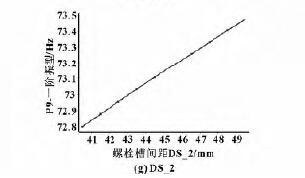
图9 一阶振型对各个输入参数的响应图
根据图8 和图9 的响应曲线可知,随着输入参数的减小,结构低阶最大振型的增大,有可能出现质量轻且低阶振型较大的情况。
2. 3. 3 立柱的多目标优化
如上所说,多目标优化得到的是一个最优解的集合。在Workbench 中的得到了3 个较优的可行方案,分别如图10 所示。

图10 优化可行解图
通过对比确定,以减重的标准选取立柱的最优方案应为图9 中所示的方案A,此方案中,减少了立柱导轨面凸台厚度、增大加强筋板的厚度,增大了立柱的振型,并通过减少立柱两侧的壁厚,使立柱的质量由原来的1 100 kg 减小到1 042. 6 kg,减少了5. 2%。
3 、结束语
通过对立柱的动态分析和参数优化可知,立柱壁厚、导轨面凸台壁厚是影响立柱整体动静态特性的主要因素。优化后的立柱的最大整体变形略有增大,但仍满足静态性能要求,而一阶振型为72. 801 Hz 增大到75. 089 Hz 满足动态性能要求,同样满足工程要求,综上所述优化减重5. 2% 后的立柱满足动态性能要求。
投稿箱:
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
更多相关信息





