摘　要：为了实现故障数据按故障机制的分类，使用竞争威布尔模型对加工中心可靠性进行评估，通过故障特
征属性和故障信息序列概念的定义，以故障信息序列表示故障，利用模糊聚类的方法对故障信息序列按故障机制
相似性进行分类；利用自助法和基于灰色预测的改进自助法实现小子样评估中威布尔模型的参数估计；通过实例
验证了该模型和方法的可用性。

  
 
      ０、　引言
 
 
      加工中心的使用性能是否稳定可靠，是用户判别产品质量好坏的重要依据，因此开展可靠性工作对制造企业赢得市场占有率具有重要意义。可靠性评估是了解产品可靠性水平的重要手段，其常用的寿命分布类型主要有指数分布、正态分布、对数正态分布和威布尔分布，威布尔分布是描述机械系统及其零部件寿命分布规律最常用的一种分布形式［１］，贾亚洲［２－３］等也证明了加工中心故障数据服从威布尔分布。对于复杂的可修系统，其故障数据一般为非独立同分布［４］，这就意味着单一的威布尔模型并不适用于加工中心的可靠性评估。对于多种故障机制并存的加工中心，常用的可靠性评估模型是混合威布尔模型和竞争威布尔模型。文献［５－７］讨论了混合威布尔模型的使用及权重、参数的估计方法，其中文献［６］证实混合分布中子分布所对应的数据是连续的顺序统计量，这明显不符合加工中心多故障机制的寿命过程。文献［８－１０］使用竞争故障模型对产品可靠性进行了评估，但都是利用完备的故障信息、针对具体的故障模式或故障过程建立竞争故障模型。

      本文使用竞争威布尔模型对加工中心可靠性进行评估，是在难以获得完备故障信息的情况下，围绕威布尔模型的物理背景和使用条件，针对故障特性本身提出故障特征属性和故障信息序列的概念及其表示方法，以故障固有的特征信息来描述故障机制之间的区别和联系。本文以故障应力相似性表征故障机制的相似性，进而实现对故障数据的分类。忽
略故障机制的差异，用单一模型拟合全部故障数据是普通威布尔模型最大的缺陷，而本文竞争威布尔模型的使用正是对这一缺陷的弥补。使用竞争威布尔模型进行可靠性评估，最重要的就是实现不同故障机制的故障数据的分类，这是竞争威布尔评估模型的基础，更是本文的核心内容；但这也导致可靠性评估必然是小子样的，本文使用自助法［１１］（ｂｏｏｔｓｔｒａｐ法）解决小子样情形下的威布尔模型参数估计问题。故障数据分类带来的另一问题是不同故障机制所对应的故障数据存在不同的截尾时间，本文利用改进灰色自助法解决这一问题，通过增加预测故障数据，很好地利用各伪截尾时间和截尾时间之间的可靠性信息，该方法也是本文的一个特点。综上所述，本文给出了利用加工中心现场故障数据、使用竞争威布尔模型进行建模评估的具体方法，主要包括基于故障特征属性的故障信息序列的建立、基于模糊聚类分析的故障数据聚类、小子样可靠性评估的Ｂｏｏｔｓｔｒａｐ法，以及用以处理伪定时截尾数据的基于灰色预测的改进Ｂｏｏｔｓｔｒａｐ法。

       １　、竞争威布尔评估模型威布尔模型的失效分布函数为

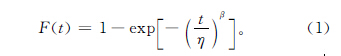
       其物理背景为：在一条金属链条两端施加一个拉力，当其中一个环断裂时，整个链条也就断裂，链条的寿命取决于最弱环的寿命长度。由此可知其适用条件为：
 
      （１）建模对象为系统组成要素的寿命长度，即建模对象应该是故障发生时间，而不是故障间隔时间。故障间隔时间是加工中心可靠性评估时最常用的特征指标，这是基于可修特性的。但是在不考虑维修影响的情况下，其故障普遍是由不同零部件损坏导致的，不相关的零部件故障的间隔时间是没有意义的。
 
      （２）系统各要素寿命独立同分布，即要求故障机制相同，至少是相似。系统寿命的分布统计，本质上是针对某种失效特性考察其平均失效时间，对于多种故障机制混合的情况，简单的统计分析没有任何意义，因为在忽略物理意义的情况下，任何一组数据都可以得到极高精度的曲线拟合。基于以上考虑，本文利用系统故障时间，采用竞争威布尔模型进行加工中心的可靠性评估。竞争威布尔模型是用不同的威布尔分布表征不同的故障机制，是对多种故障机制共同作用结果的一种描述。当有ｋ种故障机制独立地作用于系统时，其中任何一种故障机制单独作用都会引发故障，最早发生的故障将导致系统故障，即Ｔ＝ｍｉｎ｛Ｔ１，Ｔ２，…，Ｔｋ｝，这种故障形式称为竞争性故障，评估存在竞争性故
障的威布尔模型称为竞争威布尔模型。设Ｆｉ（ｔ）为Ｔｉ的累积失效分布函数，系统的累积失效分布函数为

      ２　、故障数据预处理

      加工中心的现场故障数据来源于机床生产厂家的维修记录，主要包括对故障时间、维修时间的记录和故障现象、维修方式的简单描述。由于故障记录信息不完备，来源于加工中心使用现场的故障数据无法直接归类分析。利用竞争威布尔模型进行评估，必须解决故障数据（ｔ１，ｔ２，…，ｔｎ）向ｋ 种故障机制数据（ｔ（ｉ）
１ ，…，ｔ（ｉ）ｍ ）分离的问题，故障数据的分离本质上是进行故障机制分析，然而由于信息缺乏和工作量巨大，故障机制分析是无法完成的工作。本文通过故障树分析（Ｆａｉｌｕｒｅ　Ｔｒｅｅ　Ａｎａｌｙｓｉｓ，ＦＴＡ）建立故障的特征属性集合，进而用数学的方法建立故障与故障应力的关系，以故障应力相似性表征故障机制的相似性，得出表征故障特性的故障信息序列，对故障信息序列进行模糊聚类分析，将故障数据进行分类，从而避开故障机制的分析，满足了竞争威布尔模型的要求。

      ２．１　故障特征属性和故障信息序列

      通常，故障是用故障模式、故障机制和故障应力三要素来表征的，故障机制是故障应力发生作用直到导致故障模式发生的动态或静态过程，由于机械系统的复杂性，这三要素间往往存在多种组合关系，如图１所示。在加工中心有多种故障机制，即使一个简单的零件断裂，其形成的原因和过程也不只一种，再加上故障的传递等复杂过程，故障机制很难用简单的方式或公式叙述清楚。

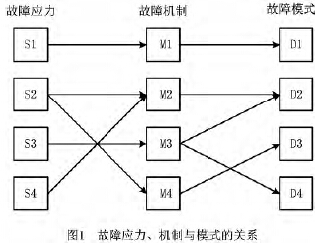
      使用威布尔模型进行系统可靠性分析，必须满足的条件是故障应力在系统各零部件上发生作用的过程一致或相近。对故障机制影响最大的因素是故障应力，相同的故障应力作用过程相似，不同的应力作用过程则肯定不同。为避免故障机制的分析，本文采用故障应力的相似性表征故障机制的相似性，用模糊评判的数学方法建立故障与故障应力之间的关系，并以模糊评判结果作为故障信息序列，以表征各故障对应的故障机制特性。

      建立故障信息序列的过程即分析不同的故障与所有故障应力之间关系的过程，为表征故障的特性，以便深入分析故障与故障应力的关系，本文定义故障特征属性为导致故障发生的随机故障事件或随机故障事件的集合。
 
 
      随机故障事件是在故障应力作用下发生的、具有一定随机性的事件，其发生不依赖于其他故障事件，但能导致其他故障事件的发生，因此随机故障事件也就是故障树分析中的底事件，而故障的特征属性就是故障树的最小割集。随机故障事件是故障应力作用的直接对象，是故障机制的发生载体，故以随机故障事件表征系统故障，能更容易得到系统故障与故障应力之间的关系。以Ｆ 表示系统故障进行ＦＴＡ 分析，得到ｎ 个导致故障Ｆ 发生的最小割集（ｆ１，ｆ２，…，ｆｎ）。以最小割集作为故障Ｆ 的特征属性，则故障Ｆ 的特殊属性集合表示为Ｆ＝（ｆ１，ｆ２，…，ｆｎ）。通过模糊评判的方法建立系统故障特征属性集合与系统故障应力集合Ｓ＝｛ｓ１，ｓ２，…，ｓｍ｝之间的关系：

      步骤１　建立故障特征属性与故障应力之间的模糊关系。利用专家知识，通过二元对比排序法，得到故障特征属性和故障应力之间的模糊关系矩阵

  
      步骤２　求得系统故障对各特征属性的评判值，并以其作为特征属性权重。利用专家打分的方式得到故障特征属性的评价值，用以表征各最小故障事件发生的可能性，并以其作为故障特征属性权重Ｗ ＝ （ｗ１，ｗ２，…，ｗｎ）。步骤３　通过模糊推理得到系统故障对故障应力的评判值，即故障信息序列。

      根据模糊变换原理，由各故障特征属性的权重值和建立的模糊关系矩阵可得故障信息序列为

   
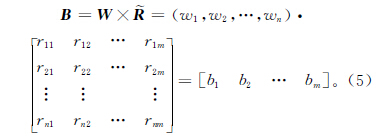
      ２．２　故障数据的模糊聚类分析

   
      以故障信息序列表征故障，信息序列中的数值表示各故障对应的故障机制的特征值，特征值的相似性标志故障机制的相似性。本文利用模糊聚类的方法分析各故障信息序列的相似性，并根据其相似性对其进行聚类分析。模糊聚类对象为故障信息序列集合｛Ｂ１，Ｂ２，…，Ｂｎ｝，其中每个对象Ｂｉ由一组数据（ｂｉ１，ｂｉ２，…，ｂｉｍ）组成，根据故障信息的相似度建立模糊相似矩阵Ａ＝（ａｉｊ）ｎ×ｎ，其中ａｉｊ表示故障Ｂｉ与Ｂｊ的相似度，

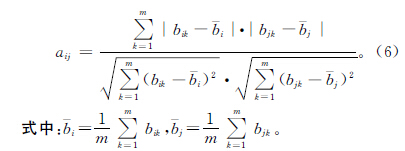
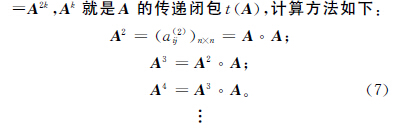
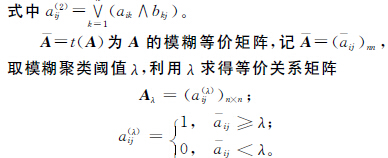
　      根据Ａλ将每列中元素１对应的Ｂ（即故障信息序列）划归为一类，从而实现故障数据按照故障机制的分类，完成竞争威布尔模型评估的故障数据预处理。

       ３、　模型参数估计

       ３．１　威布尔模型参数的自助法估计

      随着科技的进步，加工中心已具有较高的可靠性，导致评估其可靠性水平所需的有效故障数据较少，加上故障数据的分类处理，使得故障数据很难满足统计样本量的要求，即竞争威布尔模型评估必然是小子样的，本文采用自助法处理小子样评估中威布尔模型参数的估计问题。自助法是美国Ｓｔａｎｆｏｒｄ大学统计教授Ｅｆｒｏｎ提出的一种再抽样的统计方法，其主要思想是由原始观察数据经过再抽样获得含量相等的自助样本，用自助统计量与观察统计量的关系逼近观察统计量与真值之间的关系。

      利用自助法进行威布尔分布参数估计的步骤如下：

     步骤１　威布尔模型线性化。

      经过两次求对数可以得到威布尔分布的线性回归模型

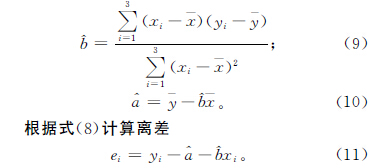
      将ｅｉ作为原始数据，利用自助法再抽样产生１　０００个自助样本。步骤３　将各个自助样本中的ｅｉ分别与对应的＾ｙｉ相加，产生１　０００个自助重复。步骤４　根据步骤２中的式（９）和式（１０）计算各自助重复的ａ和ｂ 的估计值。

      利用现场数据进行可靠性评估，对于整体故障数据（ｔ１，ｔ２，…，ｔｎ）而言，其具有定数截尾数据的特征，对（ｔ（ｉ）１ ，…，ｔ（ｉ）ｍ ）而言则具有定时截尾的特征，这是因为在ｔ（ｉ）ｍ ＜ｔ＜ｔｎ期间ｉ类故障未发生。在ｔ（ｉ）ｍ ＜ｔ＜ｔｎ期间，此种故障机制可能由于工作环境的改变而消失，也可能仍然在发生作用，但是由于工作应力或工作环境的作用，致使ｔｍ＋１（ｉ）＞ｔｎ而未被观测到。

      本文称这种具有不同于定时截尾数据特征的故障数据为伪定时截尾数据。

      ３．２　伪定时截尾数据威布尔模型参数估计伪定时截尾数据意味着存在某种故障应力在未被察觉的情况下发生作用，当条件适当时这种作用就会导致故障的发生，因此即使在考察期ｔ（ｉ）ｍ ＜ｔ＜ｔｎ内未发生故障，其对系统故障率仍具有一定贡献。为更精确地评估这种故障数据对可靠性造成的影响，本文提出基于灰色预测的改进自助法来处理截尾数据，即以添加了灰色预测故障数据的序列Ｔ′ｉ代替原始故障数据序列Ｔｉ，利用自助法进行参数估计。灰色预测法是一种对含有不确定性因素的系统进行预测的方法，灰色时间序列预测是用观察到的反映预测对象特征的时间序列来构建灰色预测模型，预测未来某一时刻的特征量。设原始序列为Ｘ（０）＝｛Ｘ（０）（１），Ｘ（０）（２），Ｘ（０）（３）｝，具体预测过程如下：

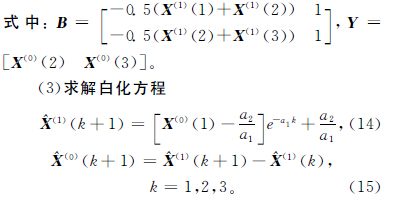
      当ｋ＝３时，由式（１４）和式（１５）求得的＾Ｘ（０）（４）即为所求。

      为更好地利用已有故障信息，本文认为对ｉ类故障机制，在ｔ（ｉ）ｍ ＜ｔ＜ｔｎ期间，故障的出现遵从非时齐泊松过程，其故障强度可以用故障率函数表示，即ｕ（ｔ）＝λ（ｔ）。通过故障强度计算期望故障数，可以确定是否需要增加预测故障数据ｔ′。基于灰色预测的改进自助法步骤为：

      ４　、实例分析

     以某型号卧式加工中心部分现场故障数据为例进行实例分析，故障集为Ｆ＝｛刀库乱刀，刀具外部冷却故障，主轴换刀故障，主轴振动异响，Ｙ 轴换刀不到位，Ｙ 轴振动异响，Ｂ 轴回转精度降低，托架交换速度过快，托架交换停止｝，故障时间为Ｔ＝｛１６５ｈ，２０７ｈ，２５４ｈ，３０７ｈ，３６６ｈ，４３６ｈ，５１１ｈ，５９１ｈ，６７８ｈ｝。根据２．１节中的方法对各故障进行故障树分析，得其故障特征属性集合，依据专家知识及模糊推理方法可得各故障信息序列为：

      根据式（６）和式（７）计算聚类对象｛Ｂ１，Ｂ２，…，Ｂｎ｝的模糊相似矩阵Ａ 的传递闭包，得

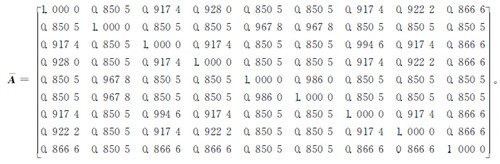
      根据模糊聚类方法，聚类阈值λ 取１，０．９９４　６，０．９８６，０．９６７　８，０．９２８，０．９２２　２，０．９１７　４，０．８６６　６，０．８５０　５，并且阈值越大分类数越多。取λ＝０．９１７　４和λ＝０．８６６　６进行计算，得等价关系矩阵如下：

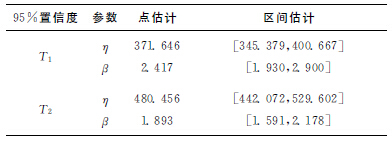
      由此可以将故障数据集分为｛ｔ１，ｔ３，ｔ４，ｔ７，ｔ８｝，｛ｔ２，ｔ５，ｔ６｝，｛ｔ９｝三类和｛ｔ１，ｔ３，ｔ４，ｔ７，ｔ８，ｔ９｝，｛ｔ２，ｔ５，ｔ６｝两类，考虑小样本数据处理的要求，选择λ＝０．８６６　６的分类作为故障数据集聚类结果，即对应于竞争威布尔分布模型中两个独立分布的故障数据，分别为Ｔ１＝｛２０７，３６６，４３６｝和Ｔ２＝｛１６５，２５４，３０７，５１１，５９１，６７８｝。在不考虑故障数据截尾影响时，由参数的自助抽样可以很容易得到其点估计和区间估计，两个威布尔分布的参数自助法估计结果如表１所示。

                           表１　Ｔ１，Ｔ２的威布尔参数估计表

      靠性指标计算如下：竞争威布尔模型故障率

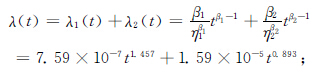
      竞争威布尔模型可靠度函数

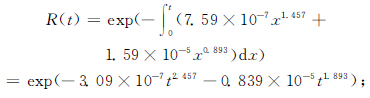
      失效密度函数

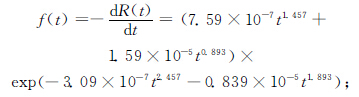
      平均无故障时间

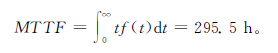
      竞争威布尔分布与普通威布尔分布可靠度函数的对比如图２所示，图中实线表示竞争威布尔模型的可靠度函数曲线，虚线表示普通单威布尔模型的可靠度函数曲线。可以发现，由于考虑故障的复杂性和故障机制的多样化，竞争威布尔模型的可靠度明显低于普通威布尔模型的计算结果，考虑到竞争性故障客观存在和“用户可靠性感受明显低于评估
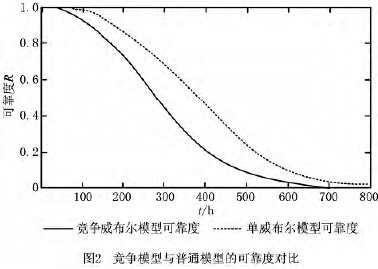
结果”的现象，笔者认为这种结果是合理的。竞争性故障是独立存在并作用于系统的，当某种故障机制的故障某时刻之后不再出现并且有足够证据表明这种故障机制消失的情况下，系统的可靠度会出现一个跳跃性的突变，如图３所示。当故障信息不足时，故障机制的消失点可以设为第３章中伪定时截尾数据处理时添加的最后一个预测故障时间ｔ（１）
５ 。

      ５　、结束语

      本文从加工中心可靠性评估中常用的威布尔模型的适用条件和物理背景出发，立足于故障机制的多样性，最终目的是实现可靠性评估的统计意义与物理意义的结合。解决了竞争威布尔模型使用受限这一难题，实现了在缺乏完备系统故障信息情况下对故障数据的分类，在遵循可靠性评估立足于故障的前提下，避免了难度大、工作量大的故障机制探测
及分析工作。本文提出的故障特征属性、故障信息序列以及伪定时截尾数据处理的概念和方法是解决本文问题的关键，是本文的创新所在，更是对研究故障特性、故障相关性和可靠性评估的有益探索。